初中数学圆幂定理解答题

如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC．已知AB＝8，CD＝2．

（1）求⊙O的半径；
（2）求sin∠BCE的值．

如图，AB是⊙O的直径，C是的中点，CE⊥AB于点E，BD交CE于点F．

（1）求证：CF=BF
（2）若CD=6，CA=8，求AE的长

如图，已知△ABC中，AC=6，∠ABC=45°．

（1）用直尺和圆规作出△ABC的外接圆（保留作图痕迹，写出结论，不写画法）；
（2）求出△ABC的外接圆半径．

如图，已知☉O的直径AB=8，过A、B两点作☉O的切线AD、BC．

（1）当AD=2，BC=8时，连接OC、OD、CD．
①求△COD的面积．
②试判断直线CD与☉O的位置关系，并说明理由．
（2）若直线CD与☉O相切于点E，设AD=x（x＞0），试用含x的式子表示四边形ABCD的面积S，并探索S是否存在最小值，写出探索过程．

已知：如图，在中，，点在上，以为圆心，长为半径的圆与分别交于点，且．

（1）判断直线与的位置关系，并证明你的结论；
（2）若，，求的长．

如图，PB为⊙O的切线，B为切点，直线PO交⊙O于点E，F，过点B作PO的垂线BA，垂足为点D，交⊙O于点A，延长AO与⊙O交于点C，连接BC，AF．

（1）求证：直线PA为⊙O的切线；
（2）求证：EF²=4OD•OP；
（3）若BC=6，tan∠F=，求AC的长．

如图，已知☉O的直径AB=8，过A、B两点作☉O的切线AD、BC．

（1）当AD=2，BC=8时，连接OC、OD、CD．
①求△COD的面积．
②试判断直线CD与☉O的位置关系，并说明理由．
（2）若直线CD与☉O相切于点E，设AD=x（x＞0），试用含x的式子表示四边形ABCD的面积S，并探索S是否存在最小值，写出探索过程．

如图，四边形OBCD中的三个顶点在⊙O上，点A是⊙O上的一个动点（不与点B、C、D重合）．

（1）若点A在优弧上，且圆心O在∠BAD的内部，已知∠BOD=120°，则∠OBA+∠ODA= °．
（2）若四边形OBCD为平行四边形．
①当圆心O在∠BAD的内部时，求∠OBA+∠ODA的度数；
②当圆心O在∠BAD的外部时，请画出图形并直接写出∠OBA与∠ODA的数量关系．

如图，在△ABC中，AB=AC，以AC为直径的⊙O交AB于点D，交BC于点E．

（1）求证：BE=CE；
（2）若∠B=70°，求弧DE的度数．
（3）若BD=2，BE=3，求AC的长．

如图，已知点C、D在以O为圆心，AB为直径的半圆上，且OC⊥BD于点M，CF⊥AB于点F交BD于点E，BD=8，CM=2．

（1）求⊙O的半径；
（2）求证：CE=BE．

如图，PB为⊙O的切线，B为切点，直线PO交⊙O于点E，F，过点B作PO的垂线BA，垂足为点D，交⊙O于点A，延长AO与⊙O交于点C，连接BC，AF．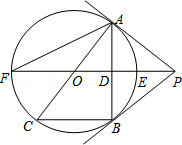

（1）求证：直线PA为⊙O的切线；
（2）求证：EF²=4OD•OP；
（3）若BC=6，tan∠F=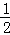，求AC的长．

如图，从一个半径为1的圆形铁皮中剪下一个圆心角为90°的扇形BAC．

（1）求这个扇形的面积；
（2）若将扇形BAC围成一个圆锥的侧面，这个圆锥的底面直径是多少？能否从最大的余料③中剪出一个圆做该圆锥的底面？请说明理由．

已知：如图，AB是⊙O的直径，点P在BA的延长线上，PD切⊙O于点C，BD⊥PD，垂足为D，连接BC．

求证：（1）BC平分∠PBD；
（2）BC²=AB•BD．

若一个三角形的三个顶点均在一个图形的不同的边上，则称此三角形为该图形的内接三角形．

（1）在图①中画出△ABC的一个内接直角三角形；
（2）如图②，已知△ABC中，∠BAC＝60°，∠B＝45°，AB＝8，AD为BC边上的高，探究以D为一个顶点作△ABC的内接三角形，其周长是否存在最小值？若存在，请求出最小值；若不存在，请说明理由；
（3）如图③，△ABC为等腰直角三角形，∠C＝90°，AC＝６，试探究：△ABC的内接等腰直角三角形的面积是否存在最小值？若存在，请求出最小值；若不存在，请说明理由．

如图，直线AB、BC、CD分别与⊙O相切于E、F、G，且AB//CD，OB＝6cm，OC＝8cm，

求：（1）∠BOC的度数；
（2）BE＋CG的长；
（3）⊙O的半径。