如图,已知☉O的直径AB=8,过A、B两点作☉O的切线AD、BC.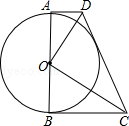
(1)当AD=2,BC=8时,连接OC、OD、CD.
①求△COD的面积.
②试判断直线CD与☉O的位置关系,并说明理由.
(2)若直线CD与☉O相切于点E,设AD=x(x>0),试用含x的式子表示四边形ABCD的面积S,并探索S是否存在最小值,写出探索过程.
相关知识点
推荐套卷
如图,已知☉O的直径AB=8,过A、B两点作☉O的切线AD、BC.
(1)当AD=2,BC=8时,连接OC、OD、CD.
①求△COD的面积.
②试判断直线CD与☉O的位置关系,并说明理由.
(2)若直线CD与☉O相切于点E,设AD=x(x>0),试用含x的式子表示四边形ABCD的面积S,并探索S是否存在最小值,写出探索过程.