已知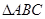 中,
中,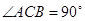 ,
, ,
, .在射线
.在射线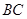 上取一点
上取一点 ,使得
,使得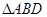 为等腰三角形,这样的三角形有几个?请你求
为等腰三角形,这样的三角形有几个?请你求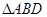 的周长.
的周长.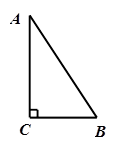
已知:如图,△AOC≌△BOD.求证:△AOD≌△BOC.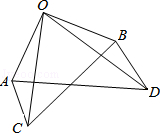
如图所示,AB是⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若AB=4,AD=1,求线段CE的长.
如图,已知直线 :
: 与直线
与直线 :y = mx-4m的图像的交点C 在第四象限,且点C到y轴的距离为2.
:y = mx-4m的图像的交点C 在第四象限,且点C到y轴的距离为2.
(1)求直线 的解析式;
的解析式;
(2)求△ADC的面积;
(3)在第一象限的角平分线上是否存在点P,使得△ADP的面积是△ADC的面积的2倍?如果存在,求出点P的坐标,如果不存在,请说明理由.
如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD、CE,两线交于点F.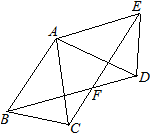
(1)求证:△ABD≌△ACE;
(2)求证:四边形ABFE是菱形.
如图,点C、F在BE上,BF=CE,AB=DE,∠B=∠E.求证:∠ACB=∠DFE.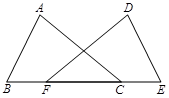
如图,在三角形ABC中,AB=AC=13,AD、BE是高,AD=12。
(1)求BC的长;(3分。)
(2)求DE的长;(2分。)
(3)求BE的长。(2分。)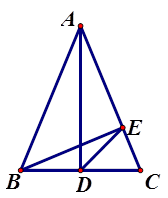
如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角板的一边交CD于点F,另一边交CB的延长线于点G.
(1)求证:EF=EG;
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变.(1)中的结论是否仍然成立?若成立,情给予证明;若不成立,请说明理由;
(本小题满分8分)如图,梯子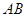 斜靠在一竖直的墙上,梯子的底端
斜靠在一竖直的墙上,梯子的底端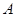 到墙根
到墙根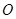 的距离
的距离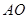 为2米,梯子的顶端B到地面的距离
为2米,梯子的顶端B到地面的距离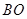 为6米.现将梯子的底端
为6米.现将梯子的底端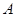 向外移动到
向外移动到 ,使梯子的底端
,使梯子的底端 到墙根
到墙根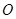 的距离
的距离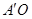 等于3米,同时梯子的顶端
等于3米,同时梯子的顶端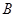 下降至
下降至 .求梯子顶端下滑的距离
.求梯子顶端下滑的距离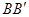 .
.