初中数学三角形的五心计算题

有一个小朋友拿着一根竹竿要通过一个长方形的门，如果把竹竿竖放就比门高出1尺，斜放就恰好等于门的对角线，已知门宽4尺，求竹竿高与门高．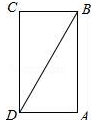

如图，在四边形ABCD中，AB=AD，AC是∠BAD的角平分线．
求证：△ABC≌△ADC．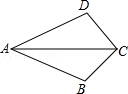

一个多边形的内角和是它的外角和的4倍，求这个多边形的边数．

如图，已知△ABC，请你按要求用尺规作出下列图形（不写作法，但要保留作图痕迹）.
（1）作出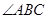的平分线BD；
（2）作出BC边上的垂直平分线EF.

已知：如图，在□ABCD中，O为对角线BD的中点，过点O的直线EF分别交AD，BC于E，F两点，连结BE，DF．

（1）求证：△DOE≌△BOF；
（2）当∠DOE满足什么条件时，四边形BEDF是菱形，说明理由．

（本小题6分）如图，在Rt△ABC中，∠ACB=90°，点D、F分别在AB、AC上，CF=CB，连接CD，将线段CD绕点C按顺时针方向旋转90°后得CE，连接EF．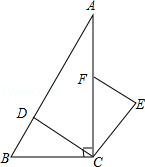

（1）求证：△BCD≌△FCE；
（2）若EF∥CD，求∠BDC的度数．

如图，在正方形ABCD中AC与BD交于点O，形外有一点E，使∠AED＝90°，且DE=3，OE=，则AE=        ．

已知：如图，E是BC上一点，AB=EC，AB∥CD，BC=CD．求证：AC=ED．

已知，如图，DE∥BC，∠A=60°，∠B=50°；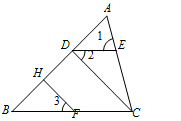

（1）求∠1的度数；
（2）若FH⊥AB于点H，且∠2=∠3，试判断CD与AB的位置关系？并加以证明．

如图，点B、F、C、E在同一直线上，∠A=∠D，BF=CE，AC∥DF．

求证：△ABC≌△DEF．

如图，A、B、C在同一直线上，且△ABD，△BCE都是等边三角形，AE交BD于点M，CD交BE于点N，求证：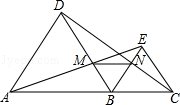

（1）∠BDN=∠BAM；
（2）△BMN是等边三角形．

如图，D、E在BC上，且BD=CE，AD=AE，求证：AB=AC．

如图1，在正方形ABCD中，E、F分别是边AD、DC上的点，且AF⊥BE．

（1）求证：AF=BE；
（2）如图2，在正方形ABCD中，M、N、P、Q分别是边AB、BC、CD、DA上的点，且MP⊥NQ．MP与NQ是否相等？并说明理由．

如图，在⊿ABC中，∠B = 50º，∠C = 70º，AD是高，AE是角平分线，

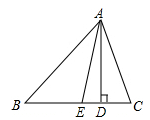
（1）∠BAC=__________,∠DAC=__________。（填度数）
（2）求∠EAD的度数．

如图，已知点在线段上，BE=CF，AB∥DE，∠ACB=∠F．求证：．