初中数学一次函数的最值解答题

小亮和小刚进行赛跑训练，他们选择了一个土坡，按同一路线同时出发，从坡底跑到坡顶再原路返回坡底．他们俩上坡的平均速度不同，下坡的平均速度则是各自上坡平均速度的1.5倍．设两人出发x min后距出发点的距离为y m．图中折线表示小亮在整个训练中y与x的函数关系，其中A点在x轴上，M点坐标为(2，0)．

小亮下坡的速度是   ▲ m/min；＝   ▲   
求出AB所在直线的函数关系式
如果小刚上坡平均速度是小亮上坡平均速度的一半，那么两人出发后多长时间第一次相遇？

某市自来水公司为了鼓励市民节约用水，于2012年4月开始采用以用户为单位按月分段收费办法收取水费，2012年3月底以前按原收费标准收费.两种收费标准见下表：

原收费标准	新按月分段收费标准
每吨2元	(1)每月用水不超过10吨（包括10吨）的用户，每吨收费1.6元； (2)每月用水超过10吨的用户，其中的10吨按每吨1.6元收费，超过10吨的部分，按每吨元收费（＞1.6）.

居民甲三月份、四月份各用水20吨，但四月份比三月份多交水费6元，求上表中 的值；
若居民甲五月份用水（吨），应交水费（元），求与之间的函数关系式,并注明自变量x的取值范围；
试问居民甲五月份用水量（吨）在什么范围内时，按新分段收费标准交的水费少于按原收费标准交的水费？

在平面直角坐标系xOy中，O为坐标原点，直线经过点A（,4）,且与轴相交于点C. 点B在轴上，且. △ABC的面积为S.
求m的取值范围;
求S关于m的函数关系式;
设点B在轴的正半轴上，当S取得最大值时，将△ABC沿AC折叠得到，求点的坐标.

某自来水公司为了鼓励市民节约用水，采取分段收费标准，若某用户居民每月应交水费y（元）是用户量x（方）的函数，其图象如图所示，根据图象回答下列问题：(10分)

（1）分别求出x≤5和x>5时，y与x的函数关系式；
（2）自来水公司的收费标准是什么？
（3）若某户居民交水费9元，该月用水多少方                                                  

有一批物资，由甲汽车从M地运往距M地180千米的N地。而甲车在驶往N地的途中发生故障，司机马上通知N地，并立即自查和维修．N地在接到通知后第12分钟时，立即派乙车前往接应．经过抢修，甲车在乙车出发第8分钟时修复并继续按原速行驶，两车在途中相遇．为了确保物资能准时运到N地，随行人员将物资全部转移到乙车上(装卸货物时间和乙车掉头时间忽略不计)，乙车按原速原路返回，并按预计时间准时到达N地．下图是甲、乙两车离N地的距离y(千米)与时间x(小时)之间的函数图象。请结合图象信息解答下列问题：

请直接在坐标系中的(  )内填上数据；
求线段CD的函数解析式，并写出
自变量x的取值范围；
求乙车的行驶速度

一个手机经销商计划购进某品牌的A型、B型、C型手机共60部，每款手机至少要购进8部，且恰好用完购机款61000元．设购进A型手机x部、三款手机的进价和预售价如下表：
手机型号 A型 B型 C型进价（单位：元/部） 900 1200 1100
预售价（单位：元/部） 1200 1600 1300
用含x的式子表示购进B、C两种型号手机的总数
该经销商共有几种进货方案；
哪种方案可获利最多，最多可获利多少元？

某电脑公司经销甲种型号电脑，受经济危机影响，电脑价格不断下降．今年三月份的电脑售价比去年同期每台降价1000元，如果卖出相同数量的电脑，去年销售额为10万元，今年销售额只有8万元．
今年三月份甲种电脑每台售价多少元
为了增加收入，电脑公司决定再经销乙种型号电脑，已知甲种电脑每台进价为3500元，乙种电脑每台进价为3000元，公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台，有几种进货方案？
如果乙种电脑每台售价为3800元，为打开乙种电脑的销路，公司决定每售出一台乙种电脑，返还顾客现金元，要使（2）中所有方案获利相同，值应是多少？此时，哪种方案对公司更有利？

如图，在平面直角坐标系中，点C（-3,0），点A、B分别在x轴，y轴的正半轴上，且满足.
求点A、B坐标
若点P从点C出发，以每秒1个单位的速度沿射线CB运动，连接AP。设△ABP面积为S，点P的运动时间为t秒，求S与t的函数关系式，并写出自变量的取值范围
在（2）的条件下，是否存在点P，使以点A、B、P为顶点的三角形与△AOB相似？若存在，请直接写出点P的坐标；若不存在，请说明理由。

某办公用品销售商店推出两种优惠方法：①购1个书包，赠送1支水性笔；②购书包和水性笔一律按9折优惠．书包每个定价20元，水性笔每支定价5元．小丽和同学需买4个书包，水性笔若干支（不少于4支）．
（1）分别写出两种优惠方法购买费用y（元）与所买水性笔支数x（支）之间的函数关系式；
（2）对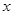的取值情况进行分析，说明按哪种优惠方法购买比较便宜；
（3）小丽和同学需买这种书包4个和水性笔12支，请你设计怎样购买最经济．

如图，一次函数y="-12" x+4的图象交x轴于点A，交正比例函数y=x的图象于点B．矩形CDEF的边DC在x轴上，D在C的左侧，EF在x轴上方，DC=2，DE=4．当点C坐标为（-2，0）时，矩形CDEF开始以每秒2个单位的速度沿x轴向右运动，运动时间为t秒．

（1）求点B的坐标．
（2）矩形CDEF运动t秒时，直接写出C、D两点的坐标．
（3）当点B在矩形CDEF的一边上时，求t的值．
（4）设CF、DE分别交折线OBA于M、N两点，当四边形MCDN为直角梯形时，求t的取范围．

某车间的李师傅每天能加工A零件25个，或B零件40个，或C零件60个，每天只能加工一种零件，每月(按22天计算)的加工定额为1000个．在刚好完成定额的前提下，请解答下列问题：
设李师傅每月用x天加工A零件，y天加工B零件，请写出y与x的函数关系式；
若每种零件每月至少加工2天，李师傅有哪几种安排加工的方案(加工天数取整数)？
若李师傅的月工资分为基本工资与计件工资两部分，其中计件工资的计算方法是：
加工1个A零件计0.5元，加工1个B零件计0.3元，加工1个C零件计0.2元．请写出计件工资w(元)与x(天)的关系式，并在(2)提供的方案中帮助李师傅选择一个最佳方案，使他的计件工资尽可能高，计件工资最多能得到多少元？

如图①，双曲线y＝（k>0）与直线y＝k'x交于A、B两点，点A在第一象限．
若点A的坐标为(4，2)，则点B的坐标为_______．若点A的横坐标为m，则点B的坐标可表示为_______．
如图②，过原点O作另一条直线l，交双曲线y＝（k>0）于P、Q两点，点P在第一
象限．①四边形APBQ的形状一定是             
②设点A、P的横坐标分别为m、n，四边形APBQ可能是矩形吗？若可能，请直接写
出m、n应满足的条件；若不可能，请说明理由．

如图，已知函数的图象与直线相交于点A（1，3）、B（，1）两点，

写出、、的值；
求不等式的解（请直接写出答案）；
求△AOB的面积。

2009年，财政部发布了“家电下乡”的政府补贴资金政策，对农民购买手机等四类家电给予销售价格13﹪的财政补贴，以提高农民的购买力. 某公司为促进手机销售，推出A、B、C三款手机，除享受政府补贴，另外每部手机赠送120元话费. 手机价格如下表：

王强买了一部C款手机，他共能获得多少优惠？
王强买回手机后，乡亲们委托他代买10部手机，设所购手机的总售价为元，两项优惠共元，请写出关于的函数关系式；这时，政府最多需付出补贴资金多少元？
根据（2）中的函数关系式，
在右边图象中填上适当的数据.

如图，在平面直角坐标中，边长为2的正方形的两顶点、分别在轴、轴的正半轴上，点在原点.现将正方形绕点顺时针旋转，旋转角为θ，当点第一次落在直线上时停止旋转．旋转过程中，边交直线于点，边交轴于点.

（1）当点第一次落在直线上时，求A、B两点坐标（直接写出结果）；
（2）设的周长为，在旋转正方形的过程中，值是否有变化？请证明你的结论.