[江苏]2012届江苏无锡南长区九年级一模考试数学卷
已知某种纸一张的厚度约为0.0089cm,用科学计数法表示这个数为 【▲】
| A.8.9×10-5 | B.8.9×10-4 | C.8.9×10-3 | D.8.9×10-2 |
下列运算中,计算正确的是 【▲】
| A.a3·a2=a6 | B.a8÷a2=a4 | C.(ab2)2=a5 | D.(a2)3=a6 |
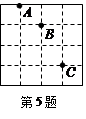
如图,在正方形的网格图中,若A(1,1),B(2,0),则C点的坐标为 【▲】
| A.(―3,―2) | B.(3,-2) | C.(―2,―3) | D.(2,-3) |
将直径为60cm的圆形铁皮,做成三个相同的圆锥容器的侧面(不浪费材料,不计接缝处的材料损耗),
那么每个圆锥容器的底面半径为 【▲】
| A.10cm | B.20cm | C.30cm | D.60cm |
某学校用420元钱到商场去购买“84”消毒液,经过还价,每瓶便宜0.5元,结果比用原价多买了20瓶,求原价每瓶多少元?若设原价每瓶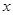 元,则可列出方程为 【▲】
元,则可列出方程为 【▲】
| A.- = 20 | B.- = 20 | C.- = 0.5 | D.- = 0.5 |
将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为 【▲】
A.15 B.28
B.28 C.29
C.29 D.34
D.34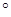
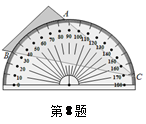
小高从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,那么他从单位到家门口需要的时间是 【▲】
| A.12分钟 | B.15分钟 | C.25分钟 | D.27分钟 |

如图,在Rt△ABC中,∠C=90°,AB=5cm,BC=3cm,动点P从点A 出发,以每秒1cm的速度,沿A→B→C的方向运动,到达点C时停止.设y=PC2,运动时间为t秒,则能反映y与t之间函数关系的大致图象是 【▲】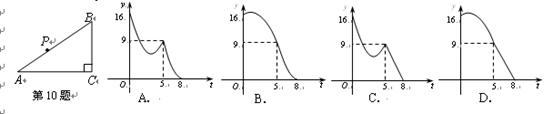
一副羽毛球拍进价提高40%后标价,然后再打八折卖出,结果仍能获利15元,为求这副羽毛球拍的进价,设这副羽毛球拍的进价为x元,则依题意列出的方程为 ▲ .
如图,是4×4的正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形,则这个白色小正方形内的数字是 ▲ .
我们知道,比较两个数的大小有很多方法,其中的图象法也非常巧妙,比如,通过图中的信息,我们可以得出x>的解是 ▲ .
计算: 2sin60°-3tan30°+()0-(-1)2012
有一道题:“先化简再求值:( + )÷,其中x=-”,小明做题时把“x=-”错抄成了“x=”,但他的计算结果也正确,请你通过计算解释这是为什么?
在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.求小明、小华各取一次小球所确定的点(x,y)落在反比例函数y= 的图象上的概率;
求小明、小华各取一次小球所确定的数x、y满足y<的概率.
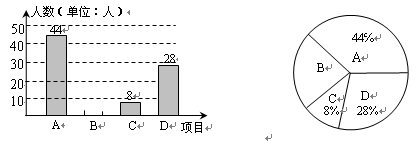
某市积极开展“阳光体育进校园”活动,各校学生坚持每天锻炼一小时,某校根据实际,决定主要开设A:乒乓球,B:篮球,C:跑步,D:跳绳四种运动项目.为了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图.请你结合图中信息解答下列问题,样本中最喜欢B项目的人数百分比是____,其所在扇形图中的圆心角的度数是__________.
请把统计图补充完整.
已知该校有1200人,请根据样本估计全校最喜欢乒乓球的人数是多少?
某晚的海滨路,小明和小亮与安装有路灯的电线杆整齐划一地排列在马路的一侧,地面上有他们两人在路灯灯光下的影子(如图1所示).在图2中,线段AB和CD分别表示小明和小亮的身高,A′B和C′D表示所对应的影子.请用尺规作图的方法,在图2作出路灯O和电线杆OP的位置(不写作法,但须保留作图痕迹);
若AB=CD=180㎝,A′ B=270㎝,C′ D=120㎝,BD=200㎝,你能否计算出路灯O的高度?若能,请求出路灯高度;若不能,说明理由.
某车间的李师傅每天能加工A零件25个,或B零件40个,或C零件60个,每天只能加工一种零件,每月(按22天计算)的加工定额为1000个.在刚好完成定额的前提下,请解答下列问题:设李师傅每月用x天加工A零件,y天加工B零件,请写出y与x的函数关系式;
若每种零件每月至少加工2天,李师傅有哪几种安排加工的方案(加工天数取整数)?
若李师傅的月工资分为基本工资与计件工资两部分,其中计件工资的计算方法是:
加工1个A零件计0.5元,加工1个B零件计0.3元,加工1个C零件计0.2元.请写出计件工资w(元)与x(天)的关系式,并在(2)提供的方案中帮助李师傅选择一个最佳方案,使他的计件工资尽可能高,计件工资最多能得到多少元?
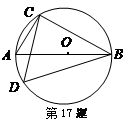
如图,△ABC内接于⊙O,D是AB边上一点,AB=6,AC=BD=4,P是的中点,连结PA、PB、PC、PD.
求证:PD=PA;
若cos∠PCB=,求PA的长.
在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.如图1,若点P在BC边上,此时PD=0,易证PD,PE,PF与AB满足的数量关系PD+PE+PF=AB;当点P在△ABC内,先在图2中作出图形,并写出PD,PE,PF与AB满足的数量关系,然后证明你的结论
当点P在△ABC外,先在图3中作出图形,然后写出PD,PE,PF与AB满足的数量关系.(不用说明理由)

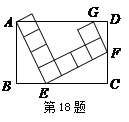
已知正方形ABCD的边长为6cm,点E是射线BC上的一个动点,连接AE交射线DC于点F,将△ABE沿直线AE翻折,点B落在点B′处.当=1时,CF=_____cm;
当 =2时,求sin∠DAB′的值;
当 =x时(点C与点E不重合),求△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式.

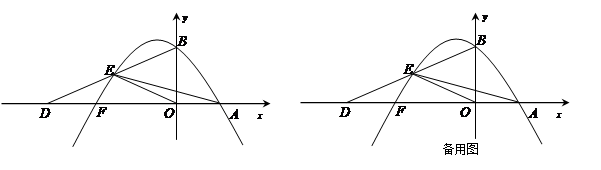
 粤公网安备 44130202000953号
粤公网安备 44130202000953号