在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.如图1,若点P在BC边上,此时PD=0,易证PD,PE,PF与AB满足的数量关系PD+PE+PF=AB;当点P在△ABC内,先在图2中作出图形,并写出PD,PE,PF与AB满足的数量关系,然后证明你的结论
当点P在△ABC外,先在图3中作出图形,然后写出PD,PE,PF与AB满足的数量关系.(不用说明理由)

相关知识点
推荐套卷
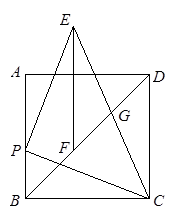
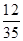 .
.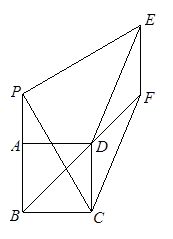
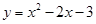 与x轴交于点A和点B,与y轴相交于点C.
与x轴交于点A和点B,与y轴相交于点C.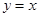 上的一个动点,点Q是抛物线上的一个动点,若以点O,C,P和Q为顶点的四边形为直角梯形,求相应的点P的坐标.
上的一个动点,点Q是抛物线上的一个动点,若以点O,C,P和Q为顶点的四边形为直角梯形,求相应的点P的坐标.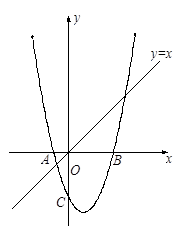
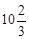 米,入水处距池边的距离为4米,运动员在距水面高度为5米以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
米,入水处距池边的距离为4米,运动员在距水面高度为5米以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.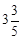 米,问此次跳水会不会失误?并通过计算说明理由.
米,问此次跳水会不会失误?并通过计算说明理由.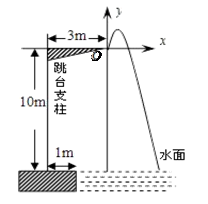

 ,求 的值
,求 的值 粤公网安备 44130202000953号
粤公网安备 44130202000953号