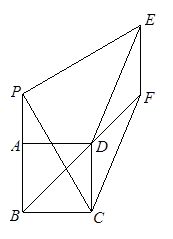如图，已知正方形ABCD，点P为射线BA上的一点（不和点A，B重合），过P作PE⊥CP，且CP＝PE．过E作EF∥CD交射线BD于F．若CB＝6，PB＝2，则EF＝ ；DF＝ ；
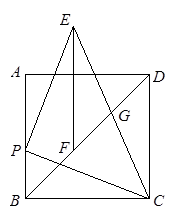
请探究BF，DG和CD这三条线段之间的数量关系，写出你的结论并证明；
如图2，点P在线段BA的延长线上，当tan∠BPC＝ 时，四边形EFCD与四边形PEFC的面积之比为
．
∥
，直线
分别交
、
，直线
交
，若
，试说明：
.
， 
，
， 0，
，
，
， 
， 
，其中
.
.
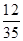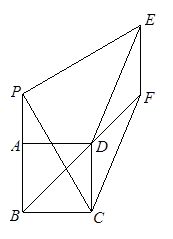
.相关知识点
推荐套卷
如图，已知正方形ABCD，点P为射线BA上的一点（不和点A，B重合），过P作PE⊥CP，且CP＝PE．过E作EF∥CD交射线BD于F．若CB＝6，PB＝2，则EF＝ ；DF＝ ；
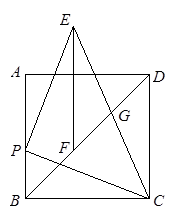
请探究BF，DG和CD这三条线段之间的数量关系，写出你的结论并证明；
如图2，点P在线段BA的延长线上，当tan∠BPC＝ 时，四边形EFCD与四边形PEFC的面积之比为
．
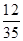粤公网安备 44130202000953号