已知一种水果的批发单价与批发量的函数关系如图(1)所示.
(1)当批发量为40千克时,批发单价为 元/千克.
(2)某经销商销售该种水果的日销量与零售价之间的函数关系如图(2)所示.
①求日销量 (千克)与零售价
(千克)与零售价 (元/千克)之间的函数关系式;
(元/千克)之间的函数关系式;
②如果经销商日销量 (千克)为整数,零售价
(千克)为整数,零售价 (元/千克)满足条件5<
(元/千克)满足条件5< <5.1
<5.1
(精确到0.01元),求经销商一天能获得的最大利润.

小明受《乌鸦喝水》故事的启发,利用量筒和体积相同的小球进行了如下操作: 请根据图中给出的信息,解答下列问题:
(1)放入一个小球量筒中水面升高_______cm;
(2)求放入小球后量筒中水面的高度y(cm)与小球个数x(个)之间的一次函数关系式(不要求写出自变量的取值范围);
(3)量筒中至少放入几个小球时有水溢出?
(4)根据上述(2)(3)小题的情况,为了不使量筒中的水溢出,请根据实际确定自变量x的取值范围,并在图2中画出自变量x在这一取值范围内水面高度y与小球个数x之间的一次函数关系的图象。
现有1240吨钢材,880吨水泥,准备用一列挂有A、B两种不同规格车厢的货车运往一城市的建筑工地。该货车有40节车厢,如果使用A型车厢每节费用为6000元,如果使用B型车厢每节费用为8000元。设运送这批钢材和水泥的总费用为y万元,这列货车挂A型车厢x节,请写出y与x之间的函数关系式。
如果每节A型车厢最多可装钢材35吨和水泥15吨,每节B型车厢最多可装钢材25吨和水泥35吨,装货时按此要求安排A、B两种车厢的节数,那么共有哪几种安排车厢的方案?
在上述方案中,哪个方案运费最少?最少运费为多少?
某农场 名职工耕种
名职工耕种 公顷土地,分别种植水稻、蔬菜和棉花,种植这些农作物每公顷所需人数如表1;另外设水稻和蔬菜的种植面积分别为
公顷土地,分别种植水稻、蔬菜和棉花,种植这些农作物每公顷所需人数如表1;另外设水稻和蔬菜的种植面积分别为 公顷、
公顷、 公顷,每公顷各种农作物预计产值如表2。
公顷,每公顷各种农作物预计产值如表2。
用含
 的式子表示
的式子表示 。
。为完成国家的粮食任务,水稻、蔬菜和棉花的种植面积至少需要12公顷,且水稻、蔬菜和棉花的种植面积均为整数,那么水稻、蔬菜和棉花的种植面积应各为多少公顷?请安排出种植方案。
若设总产值为
 ,那么怎样安排种植面积才能取得最大效益?
,那么怎样安排种植面积才能取得最大效益?
已知一次函数 中,当
中,当 时,函数值为
时,函数值为 。
。求:这个一次函数的解析式?并画出这个一次函数的图像。
求出这个函数图象与另一个正比例函数
 的交点坐标,并根据图象写出使一次函数的值大于正比例函数的值时
的交点坐标,并根据图象写出使一次函数的值大于正比例函数的值时 的取值范围。
的取值范围。
血橙以果肉酷似鲜血的颜色而得名,它本质上属脐橙类,现在已经开发出多种品种,果实一般在1月下旬成熟。由于果农在生产实践中积累了丰富的管理经验,大多采取了留树保鲜技术措施,将鲜果供应期拉长到了5月初。重庆市万州区晚熟柑橘以血橙为主,其中沙河街孙家村是万州血橙老产区,主要销售市场是成都、重庆市区、万州城区。据以往经验,孙家村上半年1~5月血橙的售价 (元/千克)与月份
(元/千克)与月份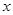 之间满足一次函数关系
之间满足一次函数关系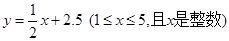 。其月销售量
。其月销售量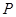 (千克)与月份
(千克)与月份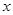 之间的相关数据如下表:
之间的相关数据如下表:
月份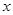 |
1月 |
2月 |
3月 |
4月 |
5月 |
销售量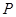 (千克) (千克) |
70000 |
65000 |
60000 |
55000 |
50000 |
请观察题中的表格,用所学过的一次函数,反比例函数或二次函数的有关知识,求月销售量
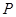 (千克)与月份
(千克)与月份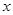 之间的函数关系式
之间的函数关系式血橙在上半年1~5月的哪个月出售,可使销售金额
 (元)最大?最大金额是多少元?
(元)最大?最大金额是多少元?由于气候适宜以及保鲜技术的提高,预计该产区今年5月将收获60000千克的血橙,并按(2)问中获得最大销售金额时的销售量售出新鲜血橙。剩下的血橙的果肉与石榴、白糖按5:2:1的比例制成“石榴·血橙白茶果冻”出售(以下简称“果冻”,制作过程中的损耗忽略不计),已知平均每千克的血橙含0.8千克的果肉。产区生产商最初将每千克果冻的批发价定为26元,超市的零售价比批发价高
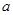 %,当销售了这批果冻的四分之三后,考虑到制作和营运成本的提高,生产商将批发价提高了
%,当销售了这批果冻的四分之三后,考虑到制作和营运成本的提高,生产商将批发价提高了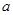 %,超市的零售价也跟着在此批发价的基础上提高了
%,超市的零售价也跟着在此批发价的基础上提高了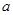 %,最后该产区将这批果冻在超市全部出售后的销售总额达到了390000元。求
%,最后该产区将这批果冻在超市全部出售后的销售总额达到了390000元。求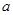 的值。(结果保留整数)
的值。(结果保留整数)
(参考数据: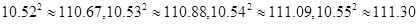 )
)
如图,在平面直角坐标系中,一次函数 与反比例函数
与反比例函数 的图象分别交于一、三象限的
的图象分别交于一、三象限的 、
、 两点,与
两点,与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,线段
,线段 点坐标为
点坐标为 ,且
,且 。
。
求该反比例函数和一次函数的解析式
求
 的面积。
的面积。
已知直线y = x+m与x轴、y轴分别交于点A、B,与双曲线y
= x+m与x轴、y轴分别交于点A、B,与双曲线y =
=  分别交于点C、D,且点C的坐标为(-1,2).
分别交于点C、D,且点C的坐标为(-1,2).分别求出直线AB及双曲线的函数表达式;
利用图像直接写出:当x在什么范围内取值时y
 >y
>y
有一个装有进水管和出水管的容器,水管的所有阀门都处于关闭状态.
初始时,打开容器的进水管,只进水;
到5分钟时,打开容器的出水管,此时既进水又出水;
到15分钟时,关闭容器的进水管,只出水;
到 分钟时,容器内的水全部排空.
分钟时,容器内的水全部排空.
已知此容器每分钟的进水量与出水量均为常数,容器内的水量 (单位:升)与时间
(单位:升)与时间 (单位:分)之间的函数关系如图所示,请根据图象回答下列问题:
(单位:分)之间的函数关系如图所示,请根据图象回答下列问题:
(1)此容器的进水管每分钟进水______升;
(2)求 时,容器内的水量
时,容器内的水量 与时间
与时间 的函数关系式;
的函数关系式;
(3)此容器的出水管每分钟出水多少升? 的值为多少?
的值为多少?
已知:直线 与
与 轴交于点A,与
轴交于点A,与 轴交于点B.
轴交于点B.分别求出A,B两点的坐标;
过A点作直线AP与
 轴交于点P,且使OP=2OB,
轴交于点P,且使OP=2OB,
求△ABP的面积.
已知:如图1,长方形ABCD中,AB=2,动点P在长方形的边BC,CD,DA上沿 的方向运动,且点P与点A,B都不重合.图2是此运动过程中,△ABP的面积
的方向运动,且点P与点A,B都不重合.图2是此运动过程中,△ABP的面积 与点P经过的路程
与点P经过的路程 之间的函数图象的一部分.
之间的函数图象的一部分.
请结合以上信息回答下列问题:
长方形ABCD中,边BC的长为________;
若长方形ABCD中,M为CD边的中点,当点P运动到与点M重合时,
 =________,
=________, =________;
=________;当
 时,
时, 与
与 之间的函数关系式是___________________;
之间的函数关系式是___________________;利用第(3)问求得的结论,在图2中将相应的
 与
与 的函数图象补充完整.
的函数图象补充完整.
(9分)如图,l1反映了某产品的销售收入与销售量之间的关系,l2反映了该产品的销售成本与销售量之间的关系,若使该产品的销售利润不低于5万元时,该产品的销售量至少达到多少吨?(销售利润=销售收入-销售成本)