已知一次函数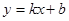 中,当
中,当 时,函数值为
时,函数值为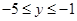 。
。求:这个一次函数的解析式?并画出这个一次函数的图像。
求出这个函数图象与另一个正比例函数
 的交点坐标,并根据图象写出使一次函数的值大于正比例函数的值时
的交点坐标,并根据图象写出使一次函数的值大于正比例函数的值时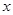 的取值范围。
的取值范围。
相关知识点
推荐套卷
已知一次函数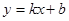 中,当
中,当 时,函数值为
时,函数值为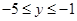 。
。求:这个一次函数的解析式?并画出这个一次函数的图像。
求出这个函数图象与另一个正比例函数
 的交点坐标,并根据图象写出使一次函数的值大于正比例函数的值时
的交点坐标,并根据图象写出使一次函数的值大于正比例函数的值时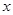 的取值范围。
的取值范围。