如图,在 中,
中,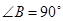 ,
,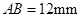 ,
, ,动点
,动点 从点
从点 开始沿边
开始沿边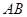 向
向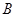 以
以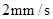 的速度移动(不与点
的速度移动(不与点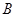 重合),动点
重合),动点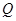 从点
从点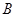 开始沿边
开始沿边 向
向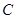 以
以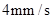 的速度移动(不与点
的速度移动(不与点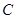 重合).如果
重合).如果 、
、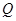 分别从
分别从 、
、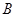 同时出发,那么经过_____________秒,四 边形
同时出发,那么经过_____________秒,四 边形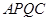 的面积最小.
的面积最小.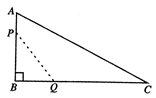
记抛物线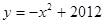 的图象与
的图象与 正半轴的交点为A,将线段OA分成2012等份,设分点分别为P1, P2,…,P2011,过每个分点作
正半轴的交点为A,将线段OA分成2012等份,设分点分别为P1, P2,…,P2011,过每个分点作 轴的垂线,分别与抛物线交于点Q1,Q2,…,Q2011,再记直角三角形OP1Q1,P1P2Q2,…的面积分别为S1,S2,…,这样就记W=S12+S22+S32+·····+S20112,W的值为
轴的垂线,分别与抛物线交于点Q1,Q2,…,Q2011,再记直角三角形OP1Q1,P1P2Q2,…的面积分别为S1,S2,…,这样就记W=S12+S22+S32+·····+S20112,W的值为
一条抛物线具有下列特征:(1)经过点A(0,3);(2)在x轴左侧的部分是上升的,在x轴右侧的部分是下降的,试写出一条满足这两条特征的抛物线的表达式: .
某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数表达式是y = 60x-1.5x2,该型号飞机着陆后需滑行 m才能停下来.
王翔同学在一次跳高训练中采用了背跃式,跳跃路线正好和抛物线y=-2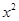 +3x+
+3x+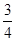 相吻合,那么他能跳过的最大高度为_________m.
相吻合,那么他能跳过的最大高度为_________m.
如图,抛物线y1=-x2+2向右平移1个单位得到的抛物线y2.回答下列问题:
(1)抛物线y2的解析式是_____,顶点坐标为_____;
(2)阴影部分的面积_____;
(3)若再将抛物线y2绕原点O旋转180°得到抛物线y3,则抛物线y3的解析式为_____,开口方向_____,顶点坐标为_____.
如图,一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O,A1;
将C1绕点A1旋转180°得C2,交x轴于点A2;
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
如此进行下去,直至得C2015.
若P(m,2),在第2015段抛物线C2015上,则m= 6043或6044 .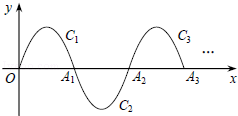
将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形面积之和的最小值是 cm2.
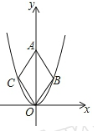
二次函数y=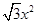 的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=
的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=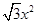 的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为 .
的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为 .
设抛物线y=-x2+8x-12与X轴的两个交点是A、B,与y轴的交点为C,则△ABC的面积是 .
如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与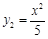 (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则 = .
= .

如图,平行于 轴的直线AC分别交抛物线
轴的直线AC分别交抛物线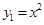 (
( ≥0)与
≥0)与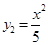 (
( ≥0)于B、C两点,过点C作
≥0)于B、C两点,过点C作 轴的平行线交
轴的平行线交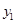 于点D,直线DE∥AC,交
于点D,直线DE∥AC,交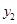 于点E,则
于点E,则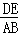 = .
= .

如图,已知抛物线C1:y=a1x2+b1x+c1和C2:y=a2x2+b2x+c2都经过原点,顶点分别为A,B,与x轴的另一个交点分别为M、N,如果点A与点B,点M与点N都关于原点O成中心对称,则抛物线C1和C2为姐妹抛物线,请你写出一对姐妹抛物线C1和C2,使四边形ANBM恰好是矩形,你所写的一对抛物线解析式是_______________________和_________________________
如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=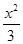 (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则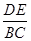 = .
= .