初中数学二次函数在给定区间上的最值填空题

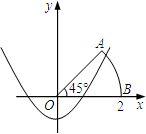
已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，则下列结论：①a+b+c＜0；②a–b+c＜0；③b+2a＜0；④abc＞0，其中正确的是             （填写正确的序号）。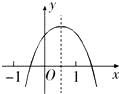

如图，抛物线y₁=-x²+2向右平移1个单位得到的抛物线y₂．回答下列问题：

（1）抛物线y₂的解析式是_____，顶点坐标为_____；
（2）阴影部分的面积_____;
（3）若再将抛物线y₂绕原点O旋转180°得到抛物线y₃，则抛物线y₃的解析式为_____，开口方向_____，顶点坐标为_____．

设抛物线y=－x²+8x－12与X轴的两个交点是A、B，与y轴的交点为C，则△ABC的面积是     ．

如图，以扇形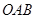的顶点为原点，半径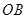所在的直线为轴，建立平面直角坐标系，点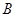的坐标为，若抛物线与扇形OAB的边界总有两个公共点，则实数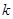的取值范围是           ．

抛物线与y轴的交点坐标为_________．

若二次函数y＝ax²－3x＋a²－1的图象开口向下且经过原点，则a的值是          ．

若抛物线y＝x²－kx＋k－1的顶点在轴上，则k＝        ．

若抛物线y＝x²－kx＋k－1的顶点在轴上，则k＝        ．

若关于x的一元二次方程（x-2）（x-3）=m有实数根x₁，x₂，且x₁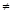x₂有下列结论：
①x₁=2，x₂=3；
②m>；
③二次函数y=（x-x₁）（x-x₂）+m的图象与x轴交点的坐标为（2，0）和（3，0）．
其中正确的结论是__________（填正确结论的序号）

如图，⊙O的半径为2，是函数的图象，是函数的图象，是函数的图象，则阴影部分的面积是         平方单位（结果保留）．

将二次函数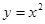的图象向右平移1个单位，再向上平移2个单位后，所得图象的表达式是                 ．

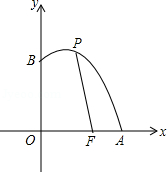
如图，已知点F的坐标为（3，0），点A，B分别是某函数图象与x轴、y轴的交点，P是此图象上的一动点．设P的横坐标为x，PF的长为d，且d与x之间满足关系：d=5﹣（0≤x≤5），给出以下四个结论：
①AF=2；②BF=5；③OA=5；④OB=4
其中正确结论的序号是      ．

已知点A（4，y₁），B（﹣2，y₂）都在二次函数y=（x﹣2）²﹣1的图象上，则y₁、y₂的大小关系是      ．（用“＜”连接）

如图，对称轴平行于y轴的抛物线与x轴交于（1，0），（3，0）两点，则它的对称轴为       ．

把抛物线y=﹣x²向上平移2个单位，那么所得抛物线与x轴的两个交点之间的距离是     ．