江苏省无锡市北塘区九年级上学期期末考试数学试卷
如果一个一元二次方程的根是x1=x2=1,那么这个方程是
| A.(x+1)2=0 |
| B.(x-1)2=0 |
| C.x2=1 |
| D.x2+1=0 |
某班抽取6名同学参加体能测试,成绩如下:80,90,75,75,80,80.下列表述错误的是
| A.平均数是80 | B.极差是15 |
| C.中位数是75 | D.方差是25 |
已知⊙O的半径是5,直线l是⊙O的切线,P是l上的任一点,那么下列结论正确的是
| A.0<OP<5 | B.OP=5 | C.OP>5 | D.OP≥5 |
二次函数y=x2-2x+3的图像的顶点坐标是
| A.(1,2) | B.(1,6) | C.(-1,6) | D.(-1,2) |
已知圆锥的底面半径为3cm,母线为5cm,则圆锥的侧面积是
| A.30πcm2 | B.15πcm2 | C. cm2 cm2 |
D.10πcm2 |
若关于x的一元二次方程x2-2x-k=0没有实数根,则k的取值范围是
| A.k>-1 | B.k≥-1 | C.k<-1 | D.k≤-1 |
如图,在Rt△ABC中,∠ACB=90°,BC=1,AB=2,下列结论正确的是
A.sinA= |
B.tanA= |
C.cosB= |
D.tanB= |
如图,⊙O的直径CD=5cm,弦AB⊥CD,垂足为M,OM︰OD=3︰5.则AB的长是……()
A.2 cm cm |
B.3cm | C.4cm | D.2 cm cm |
如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间的函数关系可用图象表示为

如图,在△ABC中,AB=AC=10,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF= ∠A,tan∠CBF=
∠A,tan∠CBF= ,则CF的长为
,则CF的长为

A. B.
B.
 C.
C. D.
D.
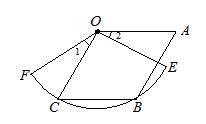
如图,四边形OABC为菱形,点B、C在以点O为圆心的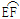 上,若OA=1cm,∠1=∠2,则
上,若OA=1cm,∠1=∠2,则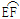 的长为 cm.
的长为 cm.
△ABC中,∠ACB=120°,AC=BC=3,点D为平面内一点,满足∠ADB=60°,若CD的长度为整数,则所有满足题意的CD的长度的可能值为 .
为了解学生参加户外活动的情况,某校对初三学生参加户外活动的时间进行抽样调查,并将调查结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)将条形统计图补画完整.
(2)求每天参加户外活动时间达到2小时的学生所占调查学生的百分比.
(3)这批参加调查的初三学生参加户外活动的平均时间是多少.
小张、小王和另两名同学一起去看电影《寻龙诀》,小张买到4张座位相连的电影票,座位号顺次为8排3、4、5、6座.现在小张和小王从中随机各抽取一张电影票,求小张和小王抽取的电影票正好是相邻座位的概率(请通过画树状图或列表法写出分析过程).
如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.
(1)△ABE与△ADF相似吗?请说明理由.
(2)若AB=6,AD=12,BE=8,求DF的长.
如图,AB是⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.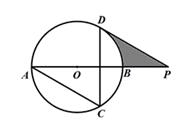
(1)求证:DP是⊙O的切线.
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
如图,小明从P处出发,沿北偏东60°方向行驶200米到达A处,接着向正南方向行驶一段时间到达B处.在B处观测到出发时所在的P处在北偏西37°方向上,这时P、B两点相距多少米?(精确到1米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, ≈1.41,
≈1.41, ≈1.73)
≈1.73)
如图,Rt△ABC中,∠C=90o,O为AB上一点,以O为圆心,OB长为半径的圆,交BC边于点D,与AC边相切于点E.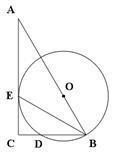
(1)求证:BE平分∠ABC;
(2)若CD︰BD=1︰2,AC=4,求CD的长.
某饰品店以20元/件的价格采购了一批今年新上市的饰品进行了为期30天的销售,销售结束后,得知日销售量P(件)与销售时间x(天)之间有如下关系:P=-2x+80(1≤x≤30);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系:Q1= x+30(1≤x≤20),后10天的销售价格Q2则稳定在45元/件.
x+30(1≤x≤20),后10天的销售价格Q2则稳定在45元/件.
(1)试分别写出该商店前20天的日销售利润R1(元)和后10天的日销售利润R2(元)与销售时间x(天)之间的函数关系式;
(2)请问在这30天的销售期中,哪一天的日销售利润最大?并求出这个最大利润值.
(注:销售利润=销售收入-购进成本)
如图,点A(-10,0),B(-6,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°.点P从点Q(8,0)出发,沿x轴向左以每秒1个单位长的速度向点A匀速运动,运动时间为t秒.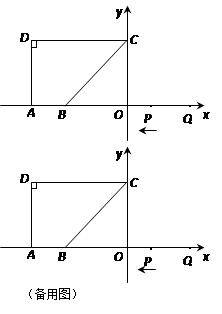
(1)求点C的坐标.
(2)当∠BCP=15°时,求t的值.
(3)以PC为直径作圆,当该圆与四边形ABCD的边(或边所在的直线)相切时,求t的值.

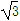 ,堤坝高BC=50m,则AB= m.
,堤坝高BC=50m,则AB= m.


 粤公网安备 44130202000953号
粤公网安备 44130202000953号