(本题13分)如图,抛物线y= - x2+
x2+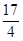 x+1与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)
x+1与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)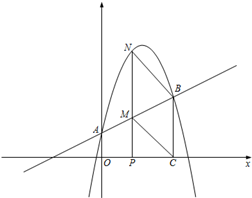
(1)求直线AB的函数关系式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N.设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?请说明理由.
如图,已知抛物线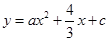 与x轴交于A、B两点,与y轴交于点C,点D在抛物线上,且A(-1,0),D(2,2).
与x轴交于A、B两点,与y轴交于点C,点D在抛物线上,且A(-1,0),D(2,2).
(1)求这条抛物线的解析式;
(2)在y轴上是否存在点P,使以O、B、P为顶点的三角形与△AOC相似,若存在,请求出点P的坐标;若不存在,请说明理由;
(3)小明在探索该图时提出了这样一个猜想:“直线AD平分∠CAB”,你认为小明的猜想正确吗?请说明理由.
抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点.
(1)求出m的值并画出这条抛物线;
(2)求它与x轴的交点和抛物线顶点的坐标;
(3)x取什么值时,抛物线在x轴上方?
(4)x取什么值时,y的值随x值的增大而减小?
如图1,P(m,n)是抛物线y= x2-1上任意一点,l是过点(0,﹣2)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H.
x2-1上任意一点,l是过点(0,﹣2)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H.
(1)填空:当m=0时,OP= ,PH= ;当m=4时,OP= ,PH= .
(2)对任意m,n,猜想OP与PH的大小关系,并证明你的猜想.
(3)连接OH,是否存在这样的点P,使得△OPH为等边三角形?如果存在,求出点P的坐标;如果不存在,请说明理由.
(4)如图2,已知线段AB=6,端点A,B在抛物线y= x2-1上滑动,求A,B两点到直线l的距离之和的最小值.
x2-1上滑动,求A,B两点到直线l的距离之和的最小值.

如图,直线y=- x+2与x轴交于点B,与y轴交于点C,已知二次函数的图象经过点B,C和点A(-1,0).
x+2与x轴交于点B,与y轴交于点C,已知二次函数的图象经过点B,C和点A(-1,0).
(1)求B,C两点坐标;
(2)求该二次函数的关系式;
(3)若抛物线的对称轴与x轴的交点为点D,点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标;
(4)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明问题.
如图,已知抛物线y=ax2+bx+c(a≠0)交x轴于A(﹣1,0),B(5,0)两点,与y轴交于点C(0,2)
(1)求抛物线的解析式;
(2)若点M为抛物线的顶点,连接BC、CM、BM,求△BCM的面积;
(3)连接AC,在x轴上是否存在点P使△ACP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
(14 分)如图,在矩形OABC 中,OA=5,AB=4,点D 为边AB 上一点,将△BCD 沿直线CD 折叠,使点B 恰好落在OA边上的点E 处,分别以OC,OA 所在的直线为x 轴,y 轴建立平面直角坐标系.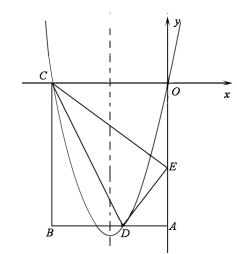
(1)求OE 的长;
(2)求经过O,D,C 三点的抛物线的解析式;
(3)一动点P 从点C 出发,沿CB 以每秒2 个单位长的速度向点B 运动,同时动点Q 从E 点出发,沿EC 以每秒1 个单位长的速度向点C 运动,当点P 到达点B 时,两点同时停止运动.设运动时间为t 秒,当t为何值时,DP=DQ;
(4)若点N 在(2)中的抛物线的对称轴上,点M 在抛物线上,是否存在这样的点M与点N,使得以M,N,C,E 为顶点的四边形是平行四边形?若存在,请求出M 点的坐标;若不存在,请说明理由.
(本小题满分12分)如图,在直角坐标系xOy中,一次函数 (m为常数)的图像与x轴交于A(-3,0),与y轴交于点C;以直线
(m为常数)的图像与x轴交于A(-3,0),与y轴交于点C;以直线 为对称轴的抛物线
为对称轴的抛物线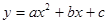 (a,b,c为常数,且a>0)经过A,C两点,与x轴正半轴交于点B.
(a,b,c为常数,且a>0)经过A,C两点,与x轴正半轴交于点B.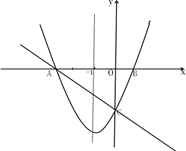
(1)求一次函数及抛物线的函数表达式。
(2)在对称轴上是否存在一点P,使得 PBC的周长最小,若存在,请求出点P的坐标.
PBC的周长最小,若存在,请求出点P的坐标.
(3)点D是线段OC上的一个动点(不与点O、点C重合),过点D作DE‖PC交x轴于点E,连接PD、PE。设CD的长为m,  PDE的面积为S。求S与m之间的函数关系式。并说明S是否存在最大值,若存在,请求出最大值:若不存在,请说明理由。
PDE的面积为S。求S与m之间的函数关系式。并说明S是否存在最大值,若存在,请求出最大值:若不存在,请说明理由。
某市是世界有机蔬菜基地,数10种蔬菜在国际市场上颇具竞争力.某种有机蔬菜上市时,某经销商按市场价格10元/千克收购了2000千克某种蔬菜存放入冷库中.据预测,该种蔬菜的市场价格每天每千克将上涨0.5元,但冷库存放这批蔬菜时每天需要支出各种费用合计340元,而且这种蔬菜在冷库中最多保存110天,同时,平均每天将会有6千克的蔬菜损坏不能出售.
(1)若存放x天后,将这批蔬菜一次性出售,设这批蔬菜的销售总金额为y元,试写出y与x之间的函数关系式.
(2)经销商想获得利润22500元,需将这批蔬菜存放多少天后出售?(利润=销售总金额-收购成本-各种费用)
(3)经销商将这批蔬菜存放多少天后出售可获得最大利润?最大利润是多少?
已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,-3).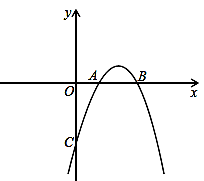
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=-x上,并写出平移后抛物线的解析式.
画出二次函数y=﹣x2+2x+3的图像,并根据图像解答下列问题:
(1)x取何值时,函数值y随x的增大而减小;
(2)x取何值时,y≤3.
某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6 000元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
如图,已知抛物线 的对称轴为直线
的对称轴为直线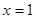 ,交
,交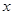 轴于
轴于 、
、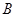 两点,交
两点,交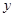 轴于
轴于 点,其中
点,其中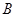 点的坐标为(3,0)。
点的坐标为(3,0)。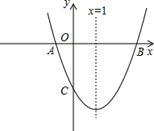
(1)直接写出 点的坐标;
点的坐标;
(2)求二次函数 的解析式。
的解析式。
(本题12分)如图,有一个长为24米的篱笆,一面利用墙(墙的最大长度a为15米)围成的中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S平方米.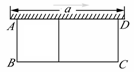
(1)求S与x的函数关系式;
(2)如果要围成花圃的面积为36平方米,求AB的长为多少米?
(3)如果要使围成花圃面积最大,求AB的长为多少米?
某商家经销一种绿茶,用于装修门面已投资3000元.已知绿茶每千克成本50元,经研究发现销量w(kg)随销售单价x(元/ kg)的变化而变化,具体变化规律如下表所示
| 销售单价x(元/ kg) |
…… |
70 |
75 |
80 |
85 |
90 |
…… |
| 月销售量w(kg) |
…… |
100 |
90 |
80 |
70 |
60 |
…… |
设该绿茶的月销售利润为y(元)(销售利润=单价×销售量-成本)
(1)请根据上表,写出w与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求y与x之间的函数关系式(不必写出自变量x的取值范围),并求出x为何值时,y的值最大?
(3)若在第一个月里,按使y获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于90元,要想在全部收回投资的基础上使第二个月的利润达到1700,那么第二个月时里应该确定销售单价为多少元?