安徽省贵池区三级教研网络中片九年级第一次联考数学试卷
已知(5,-1)是双曲线 上的一点,则下列各点中不在该图象上的是( )
上的一点,则下列各点中不在该图象上的是( )
A.( ,-15) ,-15) |
B.(5,1) | C.(-1,5) | D.(10, ) ) |
下列四个函数图象中,当x<0时,函数值y随自变量x的增大而减小的是( )
A.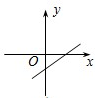 |
B.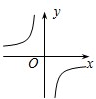 |
C.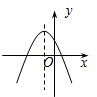 |
D.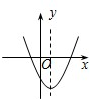 |
若△ABC∽△A′B′C′,其面积比为1:2,则△ABC与△A′B′C′的相似比为( )
| A.1:2 | B.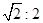 |
C.1:4 | D.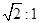 |
如图,在△ABC中,∠ADE=∠C,那么下列等式中,成立的是( )

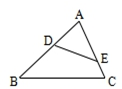
A. = = |
B.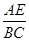 = =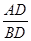 |
C.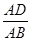 = =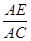 |
D. = =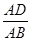 |
将抛物线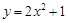 的图象向右平移2个单位,再向下平移3个单位,得到的抛物线是( )
的图象向右平移2个单位,再向下平移3个单位,得到的抛物线是( )
A.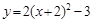 |
B.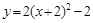 |
C.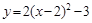 |
D.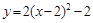 |
函数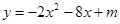 的图象上有两点
的图象上有两点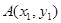 ,
,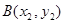 ,若
,若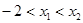 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.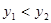 |
B.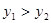 |
C.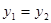 |
D.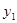 、 、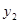 的大小不确定 的大小不确定 |
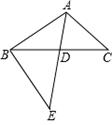
如图,△ABC中,AE交BC于点D,∠C =∠E,AD:DE = 3:5,AE=8,BD=4,则DC的长等于( )
A. |
B.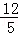 |
C.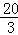 |
D.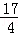 |
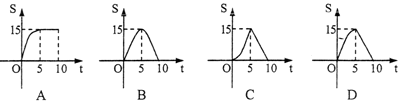
如图,△ABC中,AB=AC=10 cm,BD⊥AC于点D,且BD=6 cm,动点P从点B出发,以1 cm/s的速度,沿B→A的方向运动,到达点A时停止,动点Q从点A出发,以2cm/s的速度,沿A→C的方向运动,到达点C时停止,P、Q两点同时出发,设运动的时间为t (s),△APQ的面积为S(cm2),则S关于t的函数图象大致为( )
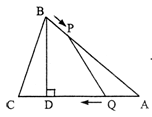
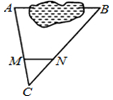
如图,A、B两点被池塘隔开,在AB外取一点C,连接AC、BC,在AC上取点M,使AM=3MC,作MN∥AB交BC于N,量得MN=38m,则AB的长为 .
如图,△ABC中,∠A=60°,BD⊥AC于点D,CE⊥AB于点E,点P为BC的中点,连接DE、PD、PE,下列结论中正确的是 .
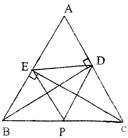
①PD=PE;
②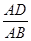 =
=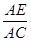 ;
;
③△PDE为等边三角形;
④当∠ABC=45°,BE=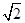 PC
PC
已知二次函数y=-x2+4x+5,完成下列各题:
(1)将函数关系式用配方法化为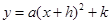 的形式,并写出它的顶点坐标、对称轴.
的形式,并写出它的顶点坐标、对称轴.
(2)求出它的图象与坐标轴的交点坐标.
(3)在直角坐标系中,画出它的图象.
(4)根据图象说明:当x为何值时,y>0;当x为何值时,y<0.
如图,点A1(1,0),过A1作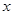 轴的垂线交直线
轴的垂线交直线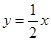 于点B1,以A1B1为边向右作正方形,在
于点B1,以A1B1为边向右作正方形,在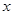 轴上一边的另一个端点为A2,过A2作
轴上一边的另一个端点为A2,过A2作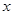 轴的长线交直线
轴的长线交直线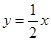 于点B2,以A2B2为右作正方形,…,依次进行下去.
于点B2,以A2B2为右作正方形,…,依次进行下去.
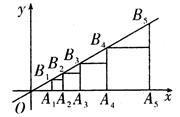
(1)第4个正方形的边长是 ,第5个正方形的边长是 ;
(2)写出点An的坐标.
如图,已知抛物线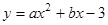 的对称轴为直线
的对称轴为直线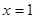 ,交
,交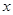 轴于A、B两点,交
轴于A、B两点,交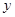 轴于C点,其中B点的坐标为(3,0).
轴于C点,其中B点的坐标为(3,0).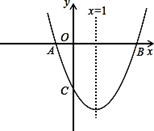
(1)直接写出A点的坐标;
(2)求二次函数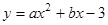 的解析式.
的解析式.
如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;
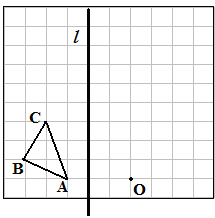
(1)先作△ABC关于直线成轴对称的图形,再向上平移1个单位,得到△A1B1C1;
(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△ A2B2C2.
如图,已知一次函数 的图象与反比例函数
的图象与反比例函数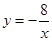 的图象交于
的图象交于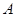 ,
, 两点,且点
两点,且点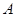 的横坐标和
的横坐标和 点的纵坐标都是
点的纵坐标都是 .
.
求:(1)一次函数解析式;
(2)求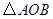 的面积.
的面积.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,点F为线段DE上一点,且∠AFE=∠B.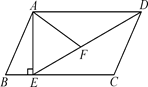
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6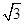 ,AF=4
,AF=4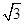 ,求AE的长.
,求AE的长.
如图,抛物线y=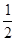 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).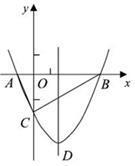
(1)求抛物线的解析式及顶点D的坐标;
(2)点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).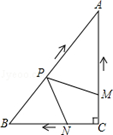
(1)当t为何值时,以A,P,M为顶点的三角形与△ABC相似?
(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.
某商家经销一种绿茶,用于装修门面已投资3000元.已知绿茶每千克成本50元,经研究发现销量w(kg)随销售单价x(元/ kg)的变化而变化,具体变化规律如下表所示
| 销售单价x(元/ kg) |
…… |
70 |
75 |
80 |
85 |
90 |
…… |
| 月销售量w(kg) |
…… |
100 |
90 |
80 |
70 |
60 |
…… |
设该绿茶的月销售利润为y(元)(销售利润=单价×销售量-成本)
(1)请根据上表,写出w与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求y与x之间的函数关系式(不必写出自变量x的取值范围),并求出x为何值时,y的值最大?
(3)若在第一个月里,按使y获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于90元,要想在全部收回投资的基础上使第二个月的利润达到1700,那么第二个月时里应该确定销售单价为多少元?
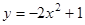 的对称轴是( )
的对称轴是( )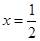
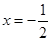
 =
=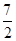
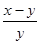 =
= 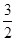
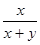 =
=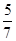
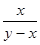 =
=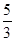
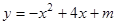 的部分图象如图所示,则关于x的一元二次方程
的部分图象如图所示,则关于x的一元二次方程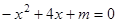 的解为 .
的解为 .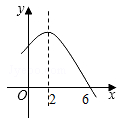
 粤公网安备 44130202000953号
粤公网安备 44130202000953号