江苏省无锡市新区九年级上学期期末考试数学试卷
已知关于 的一元二次方程m
的一元二次方程m +2x-1=0有两个不相等的实数根,则
+2x-1=0有两个不相等的实数根,则 的取值范围是( )
的取值范围是( )
| A.m<-1 | B.m>1 | C.m<1且m≠0 | D.m>-1且m≠0 |
在Rt△ABC中,∠C=90°,若AC=2,BC=1,则tanA的值是( )
A. |
B.2 | C. |
D. |
下列多边形一定相似的为( )
| A.两个三角形 | B.两个四边形 | C.两个正方形 | D.两个平行四边形 |
⊙A半径为5,圆心A的坐标为(1,0),点P的坐标为(-2,4),则点P与⊙A的位置关系是( )
| A.点P在⊙A上 | B.点P在⊙A内 |
| C.点P在⊙A外 | D.点P在⊙A上或外 |
如图,AB、AC是⊙O的两条切线,B、C是切点,若∠A = 70°,则∠BOC的度数为( )

A.100° B.110° C.120° D.130°
如图,二次函数y=ax2+bx+c的图象经过(-1,0)(0,3),下列结论中错误的是( )
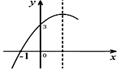
| A.abc<0 | B.9a+3b+c=0 | C.a-b=-3 | D.4ac﹣b2<0 |
二次函数y=x2的图象向上平移2个单位,得到新的图象的二次函数表达式是( )
| A.y=x2-2 | B.y=(x-2)2 |
| C.y=x2+2 | D.y=(x+2)2 |
若⊙O的直径为20cm,点O到直线l的距离为10cm,则直线l与⊙O的位置关系是( )
| A.相交 | B.相切 | C.相离 | D.无法确定 |
抛物线y=3x2,y=-3x2,y= x2+3共有的性质是( )
x2+3共有的性质是( )
| A.开口向上 | B.对称轴是y轴 |
| C.都有最高点 | D.y随x值的增大而增大 |
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:
①b2>4ac;
②abc>0;
③2a﹣b=0;
④8a+c<0;
⑤9a+3b+c<0,
其中结论正确有( )个。

| A.2个 | B.3个 | C.4个 | D.5个 |
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )

A.2 B.2
B.2 C.2
C.2 D.8
D.8
布袋中装有3个红球和6个白球,它们除颜色外其他都相同,如果从布袋里随机摸出一个球,那么所摸到的球恰好为红球的概率是____________.
已知AB为⊙O的直径AC、AD为⊙O的弦,若AB=2AC= AD,则∠DBC的度数为________.
AD,则∠DBC的度数为________.
若关于x的一元二次方程(x-2)(x-3)=m有实数根x1,x2,且x1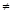 x2有下列结论:
x2有下列结论:
①x1=2,x2=3;
②m> ;
;
③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).
其中正确的结论是__________(填正确结论的序号)
居民区内的“广场舞”引起媒体关注,辽宁都市频道为此进行过专访报道.小平想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A:非常赞同;B:赞同但要有时间限制;C:无所谓;D:不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.
请你根据图中提供的信息解答下列问题:
(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)求图2中“C”层次所在扇形的圆心角的度数;
(4)估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.
如图,已知PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,若∠PAB=40°,求∠P的度数.
如图在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A、D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
(1)求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
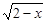 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )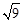 的平方根是 .
的平方根是 . =x的解是 .
=x的解是 . ,则tanB=_________.
,则tanB=_________. +6x+k=0的两个根分别是
+6x+k=0的两个根分别是 、
、 ,且
,且 ,则k的值为___________.
,则k的值为___________.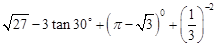
 轴和
轴和 轴分别交于A、B两点,二次函数y=
轴分别交于A、B两点,二次函数y= +bx+c的图象经过点A、B,且顶点为C.
+bx+c的图象经过点A、B,且顶点为C.
 ABP的面积为10,求点P的坐标.
ABP的面积为10,求点P的坐标. 粤公网安备 44130202000953号
粤公网安备 44130202000953号