重庆市江津区三校九年级上学期期中联考数学试卷
如图,已知△OAB是等边三角形,OC⊥OB,OC=OB,将△OAB绕点O按逆时针方向旋转,使得OA与OC重合,得到△OCD,则旋转的角度是( )

| A.150° | B.120° | C.90° | D.60° |
九年级(3)班的全体同学,在新年来临之际,在贺卡上写上自己的心愿和祝福赠送给其他同学各一张,全班共互赠了5112张,设全班有x名同学,列出的方程是( )
A. |
B. |
C. |
D. |
将正方体骰子(相对面上的点数分别为 1 和 6 、 2 和 5 、 3 和 4 )放置于水平桌面上 ,如图 ① .在图 ② 中,将骰子向右翻滚 ,然后在桌面上按逆时针方向旋转
,然后在桌面上按逆时针方向旋转 ,则完成一次变换.若骰子的初始位置为图①所示的状态,那么按上述规则连续完成100次变换后,骰子朝上一面的点数是( )
,则完成一次变换.若骰子的初始位置为图①所示的状态,那么按上述规则连续完成100次变换后,骰子朝上一面的点数是( )

| A.6 | B.5 | C.3 | D.2 |
如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:

①△BO′A可以由△BOC绕点B逆时针旋转60°得到;
②点O与O′的距离为4;
③∠AOB=150°;
④四边形AO BO′的面积为 ;
;
⑤ .
.
其中正确的结论是( )
| A.①②③ | B.①②③④ | C.①②③⑤ | D.①②③④⑤ |
如图,把矩形OABC放在直角坐标系中,OC在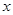 轴上,OA在
轴上,OA在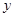 轴上,且OC=2,OA=4,把矩形OABC绕着原点顺时针旋转90度后得到矩形ODEF,则点E的坐标为_______.
轴上,且OC=2,OA=4,把矩形OABC绕着原点顺时针旋转90度后得到矩形ODEF,则点E的坐标为_______.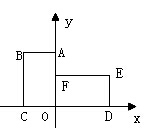
如图,平行于 轴的直线AC分别交抛物线
轴的直线AC分别交抛物线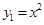 (
( ≥0)与
≥0)与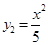 (
( ≥0)于B、C两点,过点C作
≥0)于B、C两点,过点C作 轴的平行线交
轴的平行线交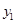 于点D,直线DE∥AC,交
于点D,直线DE∥AC,交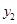 于点E,则
于点E,则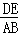 = .
= .

如图,方格纸中的每个小方格都是正方形,△ABC的顶点均在格点上,建立平面直角坐标系.

(1)以原点 为对称中心,画出与△ABC关于原点
为对称中心,画出与△ABC关于原点 对称的△A1B1C1,A1 的坐标是 .
对称的△A1B1C1,A1 的坐标是 .
(2)将原来的△ABC绕着点B顺时针旋转90°得到△A2B2C2,试在图上画出△A2B2C2的图形.
在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量 (单位:个)与销售单价
(单位:个)与销售单价 (单位:元/个)之间的对应关系如图所示:
(单位:元/个)之间的对应关系如图所示:

(1) 与
与 之间的函数关系是 .
之间的函数关系是 .
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润 (单位:元)与销售单价
(单位:元)与销售单价 (单位:元/个)之间的函数关系式;
(单位:元/个)之间的函数关系式;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.
操作:如图①,△ABC是等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角:
(1)角的两边分别交AB、AC边于M、N两点,连接MN.探究:线段BM、MN、NC之间的关系,并加以证明.
(2)若角的两边分别交AB、CA的延长线于M、N两点,连接MN。在图②中画出图形,再直接写出线段BM、MN、NC之间的关系.
小明在课外学习时遇到这样一个问题:
定义:如果二次函数 与
与 满足
满足 ,
, ,
, ,则称这两个函数互为“旋转函数”.
,则称这两个函数互为“旋转函数”.
求函数 的“旋转函数”.
的“旋转函数”.
小明是这样思考的:由函数 可知,
可知, ,
, ,
, ,根据
,根据 ,
, ,
, ,求出
,求出 ,
, ,
, ,就能确定这个函数的“旋转函数”.
,就能确定这个函数的“旋转函数”.
请参考小明的方法解决下面问题:
(1)直接写出函数 的“旋转函数”;
的“旋转函数”;
(2)若函数 与
与 互为“旋转函数”,求
互为“旋转函数”,求 的值;
的值;
(3)已知函数 的图象与
的图象与 轴交于点A、B两点(A在B的左边),与
轴交于点A、B两点(A在B的左边),与 轴交于点C,点A、B、C关于原点的对称点分别是A1,B1,C1,试证明经过点A1,B1,C1的二次函数与函数
轴交于点C,点A、B、C关于原点的对称点分别是A1,B1,C1,试证明经过点A1,B1,C1的二次函数与函数 互为“旋转函数”。
互为“旋转函数”。

 的解是( )
的解是( )



 是
是 的二次函数的是( )
的二次函数的是( )



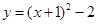 的对称轴是( )
的对称轴是( )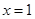
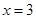
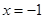
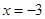




 的方程
的方程 的一个根为
的一个根为 ,则实数
,则实数 的值为( )
的值为( )
 =
= 和
和 的图象大致是( )
的图象大致是( )
 的图象如图所示,对称轴为
的图象如图所示,对称轴为 .下列结论中正确的是( )
.下列结论中正确的是( )




 的一元二次方程
的一元二次方程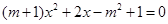 的一个根为0,则m的值___.
的一个根为0,则m的值___. 的顶点在y轴上,则b的值为__________.
的顶点在y轴上,则b的值为__________. 的
的 有实数根,则
有实数根,则 的取值范围是_______.
的取值范围是_______.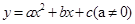 的图像如图所示,则不等式
的图像如图所示,则不等式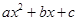 <0的解集是 .
<0的解集是 .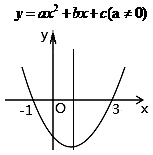
 、
、 、
、 为实数,且
为实数,且 ,求方程
,求方程 的根.
的根.
 .
. ,其中
,其中 是方程
是方程 的解.
的解. >0)与
>0)与 轴交于点C,与
轴交于点C,与 轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号