操作：如图①，△ABC是等边三角形，△BDC是顶角∠BDC＝120°的等腰三角形，以D为顶点作一个60°角：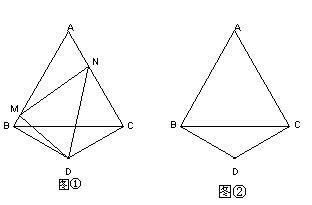
（1）角的两边分别交AB、AC边于M、N两点，连接MN．探究：线段BM、MN、NC之间的关系，并加以证明．
（2）若角的两边分别交AB、CA的延长线于M、N两点，连接MN。在图②中画出图形，再直接写出线段BM、MN、NC之间的关系．
相关试题
．
．
路线运动，到D停止；点
从
出发，沿
路线运动，到
停止．若点
的速度为
点
，
秒时点
．图②是点
的面积
与
的函数关系图象；图③点
秒后
的面积
的函数关系图象．
、c的值及点
的值；
点
请分别写出动点
改变速度后
与出发后的运动时间
相关知识点
推荐套卷
操作：如图①，△ABC是等边三角形，△BDC是顶角∠BDC＝120°的等腰三角形，以D为顶点作一个60°角：
（1）角的两边分别交AB、AC边于M、N两点，连接MN．探究：线段BM、MN、NC之间的关系，并加以证明．
（2）若角的两边分别交AB、CA的延长线于M、N两点，连接MN。在图②中画出图形，再直接写出线段BM、MN、NC之间的关系．
粤公网安备 44130202000953号