初中数学二次函数在给定区间上的最值解答题

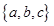定义为函数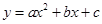的 “特征数”．如：函数y=x²－2x+3的“特征数”是{1，－2，3}，函数y=2x+3的“特征数”是{0，2，3}，函数y=－x的“特征数”是{0，－1，0}．
（1）将“特征数”是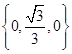的函数图象向上平移2个单位，得到一个新函数，这个函数的解析式是                       ；
（2）在（1）中，平移前后的两个函数分别与y轴交于O、A两点，与直线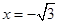分别交于C、B两点，判断以A、B、C、O四点为顶点的四边形形状，并说明理由。
（3）若（2）中的四边形（不包括边界）始终覆盖着“特征数”是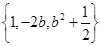的函数图象的一部分，求满足条件的实数b的取值范围？

如图1，已知抛物线y＝ax²＋bx （a≠0）经过A（3，0）、B（4，4）两点．

（1）求抛物线的解析式；
（2）将直线OB向下平移m个单位长度后，得到的直线与抛物线只有一个公共点D，求m的值及点D的坐标；
（3）如图2，若异于点A的点N在抛物线上，且∠NBO＝∠ABO，求点N的坐标；
（4）在（2）与（3）的条件下，请直接写出所有满足△POD∽△NOB的点P的坐标．

如图，已知抛物线经过A（﹣2，0），B（﹣3，3）及原点O，顶点为C

（1）求抛物线的函数解析式．
（2）设点D在抛物线上，点E在抛物线的对称轴上，且以AO为边的四边形AODE是平行四边形，求点D的坐标．
（3）P是抛物线上第一象限内的动点，过点P作PM⊥x轴，垂足为M，是否存在点P，使得以P，M，A为顶点的三角形与△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．

某桥的部分横截面如图所示，上方可看作是一个经过A、C、B三点的抛物线，以桥面的水平线为x轴，经过抛物线的顶点C与x轴垂直的直线为y轴，建立直角坐标系，已知此桥垂直于桥面的相邻两柱之间距离为2米（图中用线段AD、CO、BE等表示桥柱）CO＝1米，FG＝2米．

（1）求经过A、B、C三点的抛物线的解析式。
（2）求柱子AD的高度。

（本小题满分10分）在2014年巴西世界杯足球赛前夕，某体育用品店购进一批单价为40元的球服，如果按单价60元销售，那么一个月内可售出240套．根据销售经验，提高销售单价会导致销售量的减少，即销售单价每提高5元，销售量相应减少20套．设销售单价为x（x≥60）元，销售量为y套，当销售单价为多少元时，才能在一个

（本小题10分）已知二次函数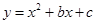（ b，c为常数）．
（Ⅰ）当b =2，c =-3时，求二次函数的最小值；
（Ⅱ）当c =5时，若在函数值y =1的情况下，只有一个自变量x的值与其对应，求此时二次函数的解析式；
（Ⅲ）当c=b²时，若在自变量x的值满足b≤x≤b+3的情况下，与其对应的函数值y的最小值为21，求此时二次函数的解析式．

已知抛物线y=ax²+bx+c的顶点为（1，0），与y轴的交点坐标为（0，）．R（1，1）是抛物线对称轴l上的一点．

（1）求抛物线y=ax²+bx+c的解析式；
（2）若P是抛物线上的一个动点（如图一），求证：点P到R的距离与点P到直线y=﹣1的距离恒相等；
（3）设直线PR与抛物线的另一交点为Q，E为线段PQ的中点，过点P、E、Q分别作直线y=﹣1的垂线．垂足分别为M、F、N（如图二）．求证：PF⊥QF．

如图，抛物线y=﹣x²﹣2x+3 的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点．

（1）求A、B、C的坐标；
（2）点M为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N．若点P在点Q左边，当矩形PQMN的周长最大时，求△AEM的面积；
（3）在（2）的条件下，当矩形PMNQ的周长最大时，连接DQ．过抛物线上一点F作y轴的平行线，与直线AC交于点G（点G在点F的上方）．若FG=2DQ，求点F的坐标．

某商店销售10台A型和20台B型电脑的利润为4000元，销售20台A型和10台B型电脑的利润为3500元．
（1）求每台A型电脑和B型电脑的销售利润；
（2）该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的2倍，设购进A型电脑x台，这100台电脑的销售总利润为y元．
①求y关于x的函数关系式；
②该商店购进A型、B型电脑各多少台，才能使销售总利润最大？
（3）实际进货时，厂家对A型电脑出厂价下调m（0＜m＜100）元，且限定商店最多购进A型电脑70台，若商店保持同种电脑的售价不变，请你根据以上信息及（2）中条件，设计出使这100台电脑销售总利润最大的进货方案．

如图，在平面直角坐标系中放置一顶点为A，B，O的直角三角形，将此三角形绕原点O顺时针旋转90°得到△A₁B₁O．抛物线y=-x²+x+2经过A，B，B₁三点．

（1）求直线A₁B₁的解析式；
（2）设点C是在抛物线上第一象限内的一点，△COB₁的面积是△ABO面积的2倍，求C点坐标；
（3）线段AB上是否存在一点P，使以点P，A₁，B为顶点的三角形与△ABO相似？若存在，请求出的值；若不存在，请说明理由．

如图，一次函数分别交y轴、x轴于A、B两点，抛物线过A、B两点．

（1）求这个抛物线的解析式；
（2）作垂直x轴的直线x=t，在第一象限交直线AB于M，交这个抛物线于N．求当t取何值时，MN有最大值？最大值是多少？

某工厂生产的某种产品按质量分为8个等级，第1等级（最低等级）的产品一天能生产85件，每件利润8元．每提高一个等级，每件利润增加2元，但一天产量减少5件．
（1）若生产第x等级的产品一天的总利润为y元（其中x为正整数，且1≤x≤8），求出y关于x的函数关系式；
（2）若生产第x等级的产品一天的总利润为900元，求该产品的质量等级．

如图，抛物线y=﹣x²+bx+c与x轴交于点A（﹣1，0），B（5，0）两点，直线y=﹣x+3与y轴交于点C，与x轴交于点D．点P是x轴上方的抛物线上一动点，过点P作PF⊥x轴于点F，交直线CD于点E．设点P的横坐标为m．

（1）求抛物线的解析式；
（2）若PE=5EF，求m的值；
（3）若点E′是点E关于直线PC的对称点，是否存在点P，使点E′落在y轴上？若存在，请直接写出相应的点P的坐标；若不存在，请说明理由．

如图，Rt△OAB中，∠OAB＝90°，O为坐标原点，边OA在x轴上，OA＝AB＝1个单位长度．把Rt△OAB沿x轴正方向平移1个单位长度后得△AA₁B．

（1）求以A为顶点，且经过点B₁的抛物线的解析式；
（2）若（1）中的抛物线与OB交于点C，与y轴交于点D，求点D、C的坐标．

如图，是坐标原点，过点的抛物线与轴的另一个交点为，与轴交于点，其顶点为点．

（1）求的值．
（2）连结、，动点的坐标为．
①当四边形是平行四边形时，求的值；
②连结、，当最大时，求出点的坐标．