如图，Rt△OAB中，∠OAB＝90°，O为坐标原点，边OA在x轴上，OA＝AB＝1个单位长度．把Rt△OAB沿x轴正方向平移1个单位长度后得△AA1B．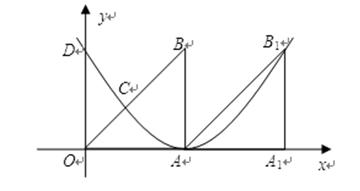
（1）求以A为顶点，且经过点B1的抛物线的解析式；
（2）若（1）中的抛物线与OB交于点C，与y轴交于点D，求点D、C的坐标．
表示3abc，方框
表示﹣4xywz，求
×
．
=
=
，求
的值．相关知识点
推荐套卷
如图，Rt△OAB中，∠OAB＝90°，O为坐标原点，边OA在x轴上，OA＝AB＝1个单位长度．把Rt△OAB沿x轴正方向平移1个单位长度后得△AA1B．
（1）求以A为顶点，且经过点B1的抛物线的解析式；
（2）若（1）中的抛物线与OB交于点C，与y轴交于点D，求点D、C的坐标．
粤公网安备 44130202000953号