如图，抛物线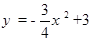
与x轴交于A，B两点，与直线
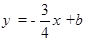相交于B，C两点，连结A，C两点。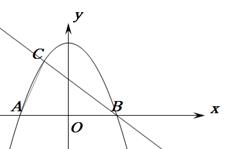 
（1）写出直线BC的解析式
（2）求△ABC的面积
已知二次函数当x=
时，有最大值
，且当x=0时，y=，求二次函数的解析式。
2015年9月19日第九届合肥文博会开幕．开幕前夕，我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销．经过调查，得到如下数据：
| 销售单价x（元/件） |
… |
20 |
30 |
40 |
50 |
60 |
… |
| 每天销售量（y件） |
… |
500 |
400 |
300 |
200 |
100 |
… |
（1）把上表中x、y的各组对应值作为点的坐标，在下面的平面直角坐标系中描出相应的点，猜想y与x的函数关系，并求出函数关系式；
（2）当销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？最大利润是多少？
（3）开幕后，合肥市物价部门规定，该工艺品销售单价最高不能超过38元/件，那么销售单价定为多少时，工艺厂销售该工艺品每天获得的利润最大？最大利润是多少？
已知抛物线y＝－x2＋2x＋2．
（1）该抛物线的对称轴是 ，顶点坐标 ；
（2）选取适当的数据填入下表，并在下图的直角坐标系内描点画出该抛物线的图象；
| x |
… |
|
|
|
|
|
… |
| y |
… |
|
|
|
|
|
… |
（3）若该抛物线上两点A（x1，y1），B（x2，y2）的横坐标满足x1＞x2＞1，试比较y1与y2的大小．
如图，一个二次函数的图象经过点A、C、B三点，点A的坐标为（
），点B的坐标为（3,0），点C在y轴的正半轴上，且AB=OC．
（1）求点C的坐标；
（2）求这个二次函数的解析式，并求出该函数的最大值．
已知二次函数y=-0．5x2+4x-3．5
（1）用配方法把该函数化为y=a(x-h)2+k的形式,并指出函数图象的对称轴和顶点坐标；
（2）求函数图象与x轴的交点坐标．
某商场将进货价为30元的台灯以40元售出，平均每月能售出600个。调查表明：这种台灯的售价每上涨一元，其销售量就将减少10个．
（1）没有涨价前每台利润是____元，月销售利润是______元．
（2）为了实现平均每月10000元的销售利润。这种台灯的售价应定为多少？这时应进台灯多少个？
如图，已知抛物线与x轴交于A（－1，0）、B（3，0）两点，与y轴交于点C（0，3）。
（1）求抛物线的解析式；
（2）若在该抛物线的对称轴上存在一点P，使得PC=PB，请求出符合条件的点P的坐标,并说明理由．
如图，在平面直角坐标系中，直线
与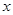
轴交于点A，与
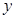轴交于点B，与抛
物线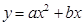
交于点C、D．已知点C的坐标为（1，7），点D的横坐标为5．
（1）求直线与抛物线的解析式；
（2）将此抛物线沿对称轴向下平移几个单位，抛物线与直线AB只有一个交点．
某商场试销一种成本为每件60元的服装，规定试销期间销售单价不能低于成本单价，且获利不得高于成本的45%，经试销发现，销售量
（件）与销售单价
（元）符合一次函数
，且
时，
；
时，
．
（1）求一次函数的表达式；
（2）若该商场获得利润为
元，试写出利润与销售单价之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？
（3）若该商场获得利润不低于500元，试确定销售单价的范围．
]已知函数y=-3（x-2）2+9
．
（1）当x= 时，抛物线有最大值，是 ；
（2）当x 时，y随x的增大而增大；
（3）该函数图象可由y=-3x2的图象经过怎样的平移得到？
（4）求出该抛物线与x轴的交点坐标；
（5）求出该抛物线与y轴的交点坐标。
已知抛物线y=ax2+bx+c经过A（﹣1，0），B（3，0），C（0，3）三点，直线L是抛物线的对称轴．
（1）求抛物线的函数关系式；
（2）求抛物线的顶点坐标；
（3）设P点是直线L上的一个动点，当△PAC的周长最小时，求点P的坐标．
（本题14分）已知抛物线
（1）填空：抛物线的顶点坐标是（ ，），对称轴是 ；
（2）已知y轴上一点A（0，-2），点P在抛物线上，过点P作PB⊥x轴，垂足为B．若△PAB是等边三角形，求点P的坐标；
（3）在（2）的条件下，点M在直线AP上．在平面内是否存在点 N，使以点O、点A、点M、点N为顶点的四边形为菱形？若存在，直接写出所有满足条件的点N的坐标；若不存在，请说明理由．
粤公网安备 44130202000953号
．
为何实数，此二次函数的图象与
轴都有两个不同交点；
有最小值
，求这个函数表达式．