河北省秦皇岛市卢龙县九年级上学期期中考试数学试卷
下列方程是一元二次方程的是( )
| A.3x2-6x+2 | B.x2-y+1=0 | C.x2=0 | D. +x=2 +x=2 |
如果关于x的一元二次方程 有两个不相等的实数根,那么
有两个不相等的实数根,那么 的取值范围是( )
的取值范围是( )
A. > > |
B. > > 且 且 |
C. < < |
D. 且 且 |
等腰三角形的底和腰是方程x2-6x+8=0的两根,则这个三角形的周长为( )
| A.8 | B.10 | C.8或10 | D.无法确定 |
抛物线 的顶点坐标是( )
的顶点坐标是( )
| A.(2,-3) | B.(-2,3) | C.(2,3) | D.(-2,-3) |
若在同一直角坐标系中,作 ,
, ,
, 的图像,则它们( )
的图像,则它们( )
A.都关于 轴对称 轴对称 |
B.开口方向相同 |
| C.都经过原点 | D.互相可以通过平移得到 |
抛物线 经过平移得到
经过平移得到 ,平移方法是( )
,平移方法是( )
| A.向右平移1个单位,再向下平移1个单位 |
| B.向右平移1个单位,再向上平移1个单位 |
| C.向左平移1个单位,再向下平移1个单位 |
| D.向左平移1个单位,再向上平移1个单位 |
如图,在长为100m,宽为80 m的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644m2,则道路的宽应为多少米?设道路的宽为x m,则可列方程为 ( )

| A.100×80-100x-80x="7644" | B.(100-x)(80-x)+x2="7644" |
| C.(100-x)(80-x)="7644" | D.100x+80x-x2=7644 |
已知实数a、b满足(a2+b2)2-2(a2+b2)=8,则a2+b2的值为( )
| A.-2 | B.4 | C.4或-2 | D.-4或2 |
已知函数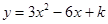 (
(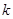 为常数)的图象经过点A(0.8,
为常数)的图象经过点A(0.8,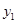 ),B(1.1,
),B(1.1,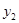 ),
),
C(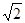 ,
,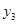 ),则有( )
),则有( )
A.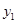 < <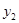 < <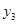 |
B.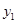 > >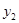 > >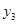 |
C.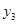 > >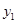 > >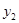 |
D.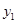 > >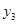 > >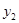 |
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:
①a+b+c<0;②a-b+c<0;③b+2a<0;④abc>0.其中所有正确结论的序号是______.
| A.②③ | B.①② | C.③④ | D.①④ |
若a-b+c=0,a≠0, 则方程ax2+bx+c=0必有一个根是____________.
某机械厂七月份生产零件50万个,第三季度生产零件196万个.设该厂八、九月份平均每月
的增长率为x,那么关于x的方程可列为 .
如图,抛物线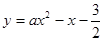 与
与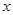 轴正半轴交于点A(3,0).以OA为边在
轴正半轴交于点A(3,0).以OA为边在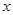 轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,点E的坐标是 .
轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,点E的坐标是 .
(本题满分14分,每小题各7分)按照要求的方法解一元二次方程
(1)3x2+4x+1=0(配方法);
(2)x2-1=3x-3(因式分解法).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,建立如图所示的平面直角坐标系,△ABC的顶点均在格点上,点B的坐标为(1,0),

(1)画出将△ABC绕原点O按顺时针旋转90°所得的△A1B1C1,并标明A1B1C1三点位置
(2)写出C1点的坐标是 ;那么C1关于原点的对称点的坐标为 .
图①②均为 的正方形网格,点
的正方形网格,点 在格点上.
在格点上.

(1)在图①中确定格点 ,并画出以
,并画出以 为顶点的四边形,使其为轴对称图形.(画出一个即可)
为顶点的四边形,使其为轴对称图形.(画出一个即可)
(2)在图②中确定格点 ,并画出以
,并画出以 为顶点的四边形,使其为中心对称图形.(画出一个即可)
为顶点的四边形,使其为中心对称图形.(画出一个即可)
.一个两位数,十位数字与个位数字之和是5,把这个两位数的个位数字与十位数字对调后,所得的新两位数与原来两位数的乘积为736,求原来的两位数.
某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润 (元)与销售单价
(元)与销售单价 (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;最大值是多少?
 的过程中,配方正确的是 ( )
的过程中,配方正确的是 ( )




 的图象的对称轴是( )
的图象的对称轴是( ) =-2
=-2 (
( 为常数)的图象如下,则
为常数)的图象如下,则 的值为( )
的值为( )



 ,则方程的解为___________.
,则方程的解为___________. 的一个根为
的一个根为 ,则另一个根为_______.
,则另一个根为_______. 与点
与点 关于原点对称,则a+b的值是_______.
关于原点对称,则a+b的值是_______.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号