初中数学二次函数在给定区间上的最值解答题

已知抛物线，
若n="-1," 求该抛物线与轴的交点坐标；
当时，抛物线与轴有且只有一个公共点，求n的取值范围．

已知：抛物线C₁：经过点A（-1，0）、B (3，0)、C（0，-3）．
（1）求抛物线C₁的解析式；
（2）将抛物线C₁向左平移几个单位长度，可使所得的抛物线C₂经过坐标原点，并求出C₂的解析式；

（3）把抛物线C₁绕点A（-1，0）旋转180°，求出所得抛物线C₃的解析式．

小明在复习数学知识时，针对“利用函数求一元二次方程的解”整理了以下几种方法，请你将有关内容补充完整：
例题：求一元二次方程的两个解。
（1）解法一：利用二次函数图象与两坐标轴的交点求解。
如图，把方程的解看成是二次函数__________的图象与轴交点的横坐标，即，就是方程的解。

（2）解法二：利用两个函数图象的交点求解。
①把方程的解看成是二次函数_________的图象与一个一次函数_________的图象交点的横坐标。
②画出这两个函数的图象，用，在轴上标出方程的解。

已知二次函数
（1）用配方法将化成的形式；
（2）在坐标系中利用描点法画出它的图象；

x	…						…
y	…						…

（3）根据图象回答：当自变量x的取值范围满足什么
条件时，随着的增大而减小？

已知：抛物线的图象经过原点，且开口向上.
确定m的值；
求此抛物线的顶点坐标；
当x取什么值时，y随x的增大而增大？
当x取什么值时，y<0？

已知二次函数y= x² ＋4x+3.
（1）用配方法将y= x² ＋4x+3化成y=a (x-h) ² +k的形式；
（2）在平面直角坐标系中，画出这个二次函数的图象；
（3）写出当x为何值时，y>0．

已知二次函数的图象与x 轴交于(2，0)、（4，0），顶点到x 轴的距离为3，求函数的解析式。

已知：抛物线C₁：经过点
、、
   <1>求抛物线C₁的解析式；
<2>将抛物线C₁向左平移几个单位长度，可使所得的抛物线C₂经过坐标原点，计算并写出C₂  的解析式；
<3>把抛物线C₁绕点A（－1，O）旋转180^o，直接写出所得抛物线C₃顶点D的坐标．

已知抛物线经过点(0 ，5)和 点(–1 ，0)，且对称轴为，求函数解析式.

已知抛物线用配方法求出它的顶点坐标、对称轴.

已知二次函数y=ax²+bx+c（a≠0）的图象过点A（2,0），B（－2，－4），对称轴为直线x=－1. （1）求这个二次函数的解析式；（2）若-3<x<3，直接写出y的取值范围；（3）若一元二次方程ax²+bx+c－m=0（a≠0，m为实数）在-3<x<3的范围内有实数根，直接写出m的取值范围.

对于抛物线y=x²－4x+3，
（1）与y轴的交点坐标是___________,与x轴的交点坐标是_______________,
顶点坐标是____________.
（2）在坐标系中利用描点法画出此抛物线.

x	...						...
y	...						...

       

已知关于x的一元二次方程有两个不等的实根，
（1）求k的取值范围；
（2）若k取小于1的整数，且此方程的解为整数，则求出此方程的两个整数根；
（3）在（2）的条件下，二次函数与x轴交于A、B两点（A点在B点的左侧），D点在此抛物线的对称轴上，若，求D点的坐标。

已知抛物线m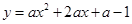：，顶点为A，若将抛物线m绕着点（1，0）旋转180°后得到抛物线n，顶点为C.
当a=1时.试求抛物线n的顶点C的坐标，再求它的解析式；
在（1）中，请你分别在抛物线m、n上各取一点D、B（除点A、C外），
使得四边形ABCD为平行四边形（直接写出所取点的坐标，并至少写出二种情况）；
设抛物线m的对称轴与抛物线n的交点为P，且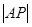=6，试求a的值.

矩形OABC的顶点A(-8，0)、C(0，6) ，点D是BC边上的中点，抛物线经过A、D两点，如图所示．
求点D关于y轴的对称点的坐标及a、b的值；
在y轴上取一点P, 使PA+PD长度最短, 求点P的坐标；
将抛物线向下平移,记平移后点A的对应点为，点D的对应点为，当抛物线平移到某个位置时，恰好使得点O是y轴上到两点距离之和最短的一点，求此抛物线的解析式．