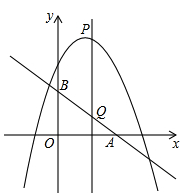
如图,已知直线y=- x+3分别交x轴、y轴于点A、B,P是抛物线y=-
x+3分别交x轴、y轴于点A、B,P是抛物线y=-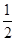 x2+2x+5上的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=-
x2+2x+5上的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=- x+3于点Q,则当PQ=BQ时,a的值是 .
x+3于点Q,则当PQ=BQ时,a的值是 .
如果将抛物线y=x2+2x-1向上平移,使它经过点A(0,3),那么所得新抛物线的表达式是_______________.
二次函数y=a(x-1)2+k(a>0)中x、y的几组对应值如下表.
| x |
-2 |
1 |
5 |
| y |
m |
n |
p |
表中m、n、p的大小关系为 (用“<”连接)
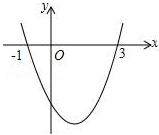
二次函数y=ax2+bx+c的图象如图所示,当函数值y<0时,自变量x的取值范围是 .
把二次函数的表达式y=x2-4x+6化为y=a(x-h)2+k的形式,那么h+k= .
在如图所示的平面直角坐标系中,桥孔抛物线对应的二次函数关系式是 ,当水位上涨1m时,水面宽CD为
,当水位上涨1m时,水面宽CD为 m,则桥下水面宽AB为____________m
m,则桥下水面宽AB为____________m 
对于抛物线y=ax2+bx+c(a≠0),有下列说法:
①当b=a+c时,则抛物线y=ax2+bx+c一定经过一个定点(-1,0);
②若△=b2-4ac>0,则抛物线y=cx2+bx+a与x轴必有两个不同的交点;
③若b=2a+3c,则抛物线y=ax2+bx+c与x轴必有两个不同的交点;
④若a>0,b>a+c,则抛物线y=ax2+bx+c与x轴必有两个不同的交点;
其中正确的有 .
已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
| x |
… |
﹣1 |
0 |
1 |
2 |
3 |
… |
| y |
… |
﹣6 |
﹣1 |
2 |
3 |
2 |
… |
则当y=﹣1时,x的取值是 。
已知抛物线y=-x²+ mx+4的顶点为D, 它与x轴交于A和B两点,且A在原点左侧,B在原点右侧,与y轴的交点为P,且以AD为直径的圆M截y轴所得的弦EF恰好以点P为中点,则m的值为 .