江苏省海安县七校九年级上学期第一次阶段性联考数学试卷

在平面直角坐标系内，点P（-3，2）关于原点的对称点Q的坐标为（ ）

如图，已知∠ACB是⊙O的圆周角，∠ACB=50°，则圆心角∠AOB是 （ ）

对于二次函数的图象，下列说法正确的是（ ）

A．开口向上

B．对称轴是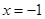

C．顶点坐标是（1，2）

D．与x轴有两个交点

在如图所示的网格中，△MNP绕某点旋转一定角度，得到△M₁N₁P₁，其旋转中心可能是（ ）

如图，在△ABC中，∠CAB＝75°．在同一平面内，将△ABC绕点A旋转到△AB′C′的位置，使得CC′∥AB，则∠BAB′＝（ ）

三角形两边长分别为3和6，第三边是方程x²-13x+36=0的根，则三角形的周长为

要将抛物线y=x²+2x+3平移后得到抛物线y=x²，下列平移方法正确的是（ ）

股票每天的涨、跌幅均不超过10%，即当涨了原价的10%后，便不能再张，叫做涨停；当跌了原价的10%后，便不能再跌，叫做跌停。已知一支股票某天跌停，之后两天时间又涨回到原价，若这两天此股票股价的平均增长率为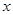，则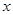满足的方程是

A．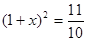

B．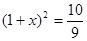

C．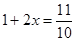

D．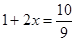

如图6，AB是⊙O的直径，AB=8，点M在⊙O上，∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点，若MN=1，则△PMN周长的最小值为（ ）．

如图，抛物线y=－x²+2x+m+1交x轴于点A（a，0）和B（b，0），交y轴于点C，抛物线的顶点为D．下列四个判断：①当x>0时，y>0；②若a=－1，则b=4；③抛物线上有两点P（x_1,y₁）和Q（x_2,y₂），若x₁<1< x₂，且x₁+ x₂>2，则y₁> y₂；④点C关于抛物线对称轴的对称点为E，点G，F分别在x轴和y轴上，当m=2时，四边形EDFG周长的最小值为，其中正确判断的序号是（）

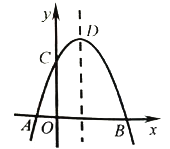
（A）①     （B）②     （C）③     （D）④

已知方程x²+mx+3=0的一个根是1，则它的另一个根是          ，m的值是         ．

关于x的方程kx2﹣4x﹣=0有实数根，则k的取值范围是         ．

已知点P坐标为（1，1），将点P绕原点逆时针旋转45°得点P₁，则点P₁的坐标为         ．

如果将抛物线y＝x²＋2x－1向上平移，使它经过点A（0，3），那么所得新抛物线的表达式是_______________．

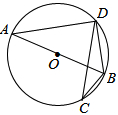
如图，已知⊙O是△ABD的外接圆，AB是⊙O的直径，CD是⊙O的弦，∠ABD＝58°，则∠BCD的度数是              ．

如图，在平面直角坐标系中，⊙E与两坐标轴分别交于A、B、C、D四点，已知A（6，0），C（－2，0），则B点坐标为           ．

如图，已知AB=AC=AD，∠CBD=2∠BDC，∠BAC=44°，则∠CAD的度数为   

如图，已知直线y=-x+3分别交x轴、y轴于点A、B，P是抛物线y=-x²+2x+5上的一个动点，其横坐标为a，过点P且平行于y轴的直线交直线y=-x+3于点Q，则当PQ=BQ时，a的值是                  ．

解方程：
（1）（x-2）²-5=0；    
（2）2x²－8x＋3＝0．

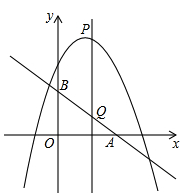
已知关于x的方程x²-2（k+1）x+k²=0有两个不相等的实数根．
（1）求k的取值范围；
（2）求证：x=-1不可能是此方程的实数根．

已知二次函数
（1）求它的顶点坐标和对称轴；
（2）画出这个函数的图象；
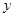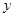（3）根据图象回答：当取哪些值时，＝0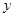，＞0，＜0

如图是规格为8×8的正方形网格，请你在所给的网格中按下列要求操作：

（1）请在网格中建立直角坐标系，使A点坐标为（4，－2），B点坐标为（2，－4），C点的坐标为（1，－1）；
（2）画出△ABC以点C为旋转中心，旋转180°后的△A₁B₁C，连接AB₁和A₁B，试写出四边形ABA₁B₁是何特殊四边形，并说明理由．

如图，AB是⊙O的直径，弦BC长为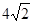，弦AC长为2，∠ACB的平分线交⊙O于点D，求AB和AD的长．

如图，AB是⊙O的直径，弦CD⊥AB于点E，点M在⊙O上，MD恰好经过圆心O，连接MB．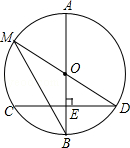

（1）若CD＝16，BE＝4，求⊙O的半径；
（2）若∠M＝∠D，求∠D的度数．

如图，四边形ABCD内接于⊙O，点E在对角线AC上，EC=BC=DC

（1）若∠CBD=39°，求∠BAD的度数
（2）求证：∠1=∠2

瓦甸科星化工有限公司购进一种化工原料若干千克，价格为每千克30元．物价部门规定其销售单价不高于每千克60元，不低于每千克30元．经市场调查发现：日销售量y（千克）是销售单价x（元）的一次函数，且当x=60时 ，y=80；x=50时，y=100．在销售过程中，每天还要支付其他费用450元．
（1）求出y与x的函数关系式，并写出自变量x的取值范围
（2）求该公司销售该原料日获利w（元）与销售单价x（元）之间的函数关系式．
（3）当销售单价为多少元时，该公司日获利最大？最大获利是多少元？ 

在数学兴趣小组活动中，小明进行数学探究活动，将边长为2的正方形ABCD与边长为2的正方形AEFG按图1位置放置，AD与AE在同一直线上，AB与AG在同一直线上．
（1）小明发现DG⊥BE，请你帮他说明理由．
（2）如图2，小明将正方形ABCD绕点A逆时针旋转，当点B恰好落在线段DG上时，请你帮他求出此时BE的长．
（3）如图3，小明将正方形ABCD绕点A继续逆时针旋转，线段DG与线段BE将相交，交点为H，写出△GHE与△BHD面积之和的最大值，并简要说明理由．

如图，在直角坐标系中，抛物线经过点A（0，4），B（1，0），C（5，0），其对称轴与x轴相交于点M．

（1）求抛物线的解析式和对称轴；
（2）在抛物线的对称轴上是否存在一点P，使△PAB的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由；
（3）连接AC，在直线AC的下方的抛物线上，是否存在一点N，使△NAC的面积最大？若存在，请求出点N的坐标；若不存在，请说明理由．