江苏省南通市海安县李堡镇初中九年级上学期期中数学试卷
已知OA=5cm,以O为圆心,r为半径作⊙O.若点A在⊙O内,则r的值可以是
| A.3cm | B.4cm | C.5cm | D.6cm |
如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于

A.55° B.70° C.125° D.145°
近年来全国房价不断上涨,某市2013年的房价平均每平方米为7000元, 经过两年的上涨,2015年房价平均每平方米为8500元,假设这两年房价的平均增长率均为 ,则关于
,则关于 的方程为
的方程为
A. |
B. |
C. |
D. |
一抛物线和抛物线y=-2x2的形状、开口方向完全相同,顶点坐标是(-1,3),则该抛物线的解析式为
| A.y=-2(x-1)2+3 | B.y=-(2x+1)2+3 |
| C.y=-2(x+1)2+3 | D.y=-(2x-1)2+3 |
如图,将△ABC绕点C(0,-1)旋转180°得到△A′B′C,设点A的坐标为(-3,-4)则点A′的坐标为
| A.(3,2) | B.(3,3) | C.(3,4) | D.(3,1) |
若x1,x2(x1<x2)是方程(x -a)(x-b)= 1(a < b)的两个根,则实数x1,x2,a,b的大小关系为
| A.x1<x2<a<b | B.x1<a<x2<b |
| C.x1<a<b<x2 | D.a<x1<b<x2 |
如图,二次函数y=ax2+bx+c的图象的顶点在第一象限,且过点(0,1)和(-1,0).下列结论:①ab<0, ②b2>4a, ③0<b<1, ④0<a+b+c<2, ⑤当x>-1时,y>0. 其中正确结论的个数是
| A.2个 | B.3个 | C.4个 | D.5个 |
下列说法:
(1)直角三角形的两边长分别为3和4,则三角形的外接圆直径是5;
(2)点A、B、C在⊙O上,∠BOC=100°,则∠A=50°或130°;
(3)各角都相等的圆的内接多边形是正多边形;
(4)平面内有四个点A、O、B、C,其中∠AOB=120°,∠ACB=60°,AO=BO=3,则OC长度为整数值的个数是4个.其中正确结论的个数是
A.1个 B.2个 C.3个 D.4个
已知正三角形的边长为a,其内切圆半径为r,外接圆半径为R,则r:R:a=___________.
如图,在⊙O的内接四边形ABCD中,AB=AD,∠BCD=140°.若点E在弦AB所对的劣弧上,则∠E=__________°.
在Rt△ABC中,∠C=90°,AC=3,BC=4.若以C点为圆心,r为半径所作的圆与斜边AB
只有一个公共点,则r的取值范围是______.
已知抛物线y=-x²+ mx+4的顶点为D, 它与x轴交于A和B两点,且A在原点左侧,B在原点右侧,与y轴的交点为P,且以AD为直径的圆M截y轴所得的弦EF恰好以点P为中点,则m的值为 .
如图所示, 是⊙O的一条弦,
是⊙O的一条弦, ,垂足为
,垂足为 ,交⊙O于点
,交⊙O于点 ,点
,点 在⊙O
在⊙O
上.
(1)若 ,求
,求 的度数;
的度数;
(2)若 ,
, ,求
,求 的长.
的长.
已知关于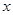 的一元二次方程x2-4x+k+1=0
的一元二次方程x2-4x+k+1=0
(1)若 =-1是方程的一个根,求k值和方程的另一根;
=-1是方程的一个根,求k值和方程的另一根;
(2)设x1,x2是关于x的方程x2-4x+k+1=0的两个实数根,是否存在实数k,使得x1x2>x1+x2成立?请说明理由.
如图,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC, 若点A对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
在平面直角坐标系中,O为坐标原点,抛物线y=-x2+kx+4与y轴交于A,与x轴的负半轴交于B,且△ABO的面积是8.
(1)求点B的坐标和此二次函数的解析式;
(2)当y≤4时,直接写出x的取值范围.
如图四边形ABCD内接于⊙O ,BD是⊙O 的直径,AE⊥CD,垂足为E,DA平分∠BDE.
(1)求证:AE是⊙O 的切线;
(2)若∠DBC=30°,DE=1cm,求BD的长.
为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=-2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
以O为圆心的两个同心圆中,AD是大圆的直径,大圆的弦AB与小圆相切于点C,过C
点作FH⊥AD交大圆于F、H,垂足为E.
(1)判断AC与BC的大小关系,并说明理由.
(2)如果FC、CH的长是方程x2-2 x+4=0的两根(CH>CF),求CE、CA的长以及图中阴影部分的面积.
x+4=0的两根(CH>CF),求CE、CA的长以及图中阴影部分的面积.
如图,把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,
斜边AB=6cm,DC=7cm,把三角板DCE绕点C顺时针旋转15°得到△D′CE′,如图乙.这时AB与CD′相交于点O,D′E′与AB相交于点F,连接AD′.
(1)求∠OFE′的度数;
(2)求线段AD′的长;
(3)若把三角形D′C E′ 绕着点C顺时针再旋转30°得△D2CE2,这时点B在△D2CE2 的内部、外部、还是边上?证明你的判断.
在平面直角坐标系中,已知抛物线y=ax2-2x+c(a,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(﹣4,3),直角顶点B在第二象限.
(1)如图,若该抛物线过A,B两点,求该抛物线的函数表达式;
(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q,判断线段PQ的长度是否为定值?如果是,求出PQ的长;如果不是,说明理由;
(3)在(2)的条件下,若点M在直线AC下方,且为平移前(1)中的抛物线上的点,以M、P、Q三点为顶点的三角形是等腰直角三角形,求出所有符合条件的点M的坐标.
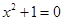
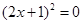
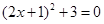
 x.
x. 粤公网安备 44130202000953号
粤公网安备 44130202000953号