如图,把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,
斜边AB=6cm,DC=7cm,把三角板DCE绕点C顺时针旋转15°得到△D′CE′,如图乙.这时AB与CD′相交于点O,D′E′与AB相交于点F,连接AD′.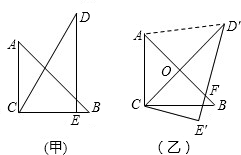
(1)求∠OFE′的度数;
(2)求线段AD′的长;
(3)若把三角形D′C E′ 绕着点C顺时针再旋转30°得△D2CE2,这时点B在△D2CE2 的内部、外部、还是边上?证明你的判断.
相关知识点
推荐套卷
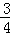 .
.
 ,
,
 (k1>0)与一次函数
(k1>0)与一次函数 相交于A、B两点,AC⊥x轴于点C.若△OAC的面积为1,且tan∠AOC=2 .
相交于A、B两点,AC⊥x轴于点C.若△OAC的面积为1,且tan∠AOC=2 .

 粤公网安备 44130202000953号
粤公网安备 44130202000953号