已知:抛物线C1: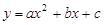 经过点A(-1,0)、B (3,0)、C(0,-3).
经过点A(-1,0)、B (3,0)、C(0,-3).
(1)求抛物线C1的解析式;
(2)将抛物线C1向左平移几个单位长度,可使所得的抛物线C2经过坐标原点,并求出C2的解析式;
|
(3)把抛物线C1绕点A(-1,0)旋转180°,求出所得抛物线C3的解析式.
相关知识点
推荐套卷
已知:抛物线C1: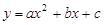 经过点A(-1,0)、B (3,0)、C(0,-3).
经过点A(-1,0)、B (3,0)、C(0,-3).
(1)求抛物线C1的解析式;
(2)将抛物线C1向左平移几个单位长度,可使所得的抛物线C2经过坐标原点,并求出C2的解析式;
|
(3)把抛物线C1绕点A(-1,0)旋转180°,求出所得抛物线C3的解析式.