.矩形的长和宽分别是4cm, 3cm ,如果将长和宽都增加x cm ,那么面积增加ycm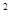
求y与x之间的关系式.
求当边长增加多少时,面积增加8 cm
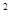
(本题满分8分)
某隧道横断面由抛物线与矩形的三边组成,尺寸如图所示,某卡车空车时能通过此隧道,现装载一集装箱箱宽3 ,车与箱共高4.5
,车与箱共高4.5 ,此车能否通过此隧道?
,此车能否通过此隧道?
体育测试时,初三一名高个学生推铅球,已知铅球所经过的路线为抛物线 的一部分,根据关系式回答:
的一部分,根据关系式回答: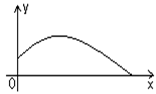
该同学的出手最大高度是多少?
铅球在运行过程中离地面的最大高度是多少?
该同学的成绩是多少?
如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D
求该抛物线的解析式与顶点D的坐标
以B、C、D为顶点的三角形是直角三角形吗?为什么?
探究
 轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,直接写出点P的坐标;若不存在,请说明理由
轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,直接写出点P的坐标;若不存在,请说明理由
如图11所示,已知抛物线 与
与 轴交于A、B两点,与
轴交于A、B两点,与 轴交于点C.
轴交于点C.
求A、B、C三点的坐标
过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积.
在
 轴上方的抛物线上是否存在一点M,过M作MG
轴上方的抛物线上是否存在一点M,过M作MG
 轴于点G,使以A、M、G三点为顶点的三角形与
轴于点G,使以A、M、G三点为顶点的三角形与 PCA相似.若存在,请求出M点的坐标;否则,请说明理由.
PCA相似.若存在,请求出M点的坐标;否则,请说明理由.
如图,已知:抛物线 ,
, 关于
关于 轴对称;抛物线
轴对称;抛物线 ,
, 关于
关于 轴对称。
轴对称。
如果抛物线 的解析式是
的解析式是 ,那么抛物线
,那么抛物线 的解析式
的解析式
是 .
已知直角梯形纸片OABC在平面直角坐标系中的位置如图①所示,四
个顶点的坐标分别为O(0,0),A(10,0),B(8,2 ),C(0,2
),C(0,2 ),点P在线段OA上(不与O、A重合),将纸片折叠,使点A落在射线AB上(记为点A’),折痕PQ与射线AB交于点Q,设OP=x,折叠后纸片重叠部分的面积为y.(图②供探索用)
),点P在线段OA上(不与O、A重合),将纸片折叠,使点A落在射线AB上(记为点A’),折痕PQ与射线AB交于点Q,设OP=x,折叠后纸片重叠部分的面积为y.(图②供探索用)求∠OAB的度数;
求y与x的函数关系式,并写出对应的x的取值范围;
y存在最大值吗?若存在,求出这个最大值,并求此时x的值;若不存在,说明理由.
)图①中是一座钢管混凝土系杆拱桥,桥的拱肋ACB可视为抛物线的一部分(如图②),桥面(视为水平的)与拱肋用垂直于桥面的系杆连接,测得拱肋
的跨度AB为200米,与AB中点O相距20米处有一高度为48米的系杆.求正中间系杆OC的长度;
若相邻系杆之间的间距均为5米(不考虑系杆的粗细),则是否存在一根系杆的长度恰好是OC长度的一半?请说明理由.

已知二次函数y=ax2+2x+c,函数y与自变量x的部分对应值如下表:
| x |
…… |
-2 |
-1 |
0 |
1 |
2 |
…… |
| y |
…… |
-5 |
0 |
3 |
4 |
3 |
…… |
求这个二次函数的关系式;
请判断函数有最大值还是最小值,并写出此时x的值与y的值;
若y≥0,则x的取值范围是_______.
若A(n,y1)、B(n+1,y2)两点均在该函数的图象上,试比较y1与y2大小.
(本小题满分5分)二次函数 中,自变量
中,自变量 与函数
与函数 的对
的对
| x |
-1 |
- |
0 |
 |
1 |
 |
2 |
 |
3 |
|
| y |
-2 |
- |
1 |
 |
2 |
 |
1 |
- |
-2 |
应值如表:判断二次函数图像的开口方向,写出它的顶点坐标。
一元二次方程
 的两个根
的两个根 的取值范围是下
的取值范围是下
列选项中的哪一个____________
① ②
②
③ ④
④
按右图的流程,输入一个数据x,根据y与x的函数关系式就 输出一个数据y,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20到100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:
(ⅰ)、新数据都在60到100(含60和100)之间。
(ⅱ)、新数据之间的大小关系与原数据之间的大小关系一致,即原数据大的对应的新数据也较大。问:若y与x的关系式是 y=x+p(100-x),请说明:当p=
 时,这种变换满足上述两个要求。
时,这种变换满足上述两个要求。若按关系式:y=a(x-h)2+k(a﹥0)将数据进行变换,请写出一个满足上述要求的这种关系式。(不要求对关系式符合题意作说明,但要求写出关系式得出的主要过程)

如图,已知抛物线 经过点
经过点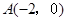 ,抛物线的顶点为
,抛物线的顶点为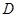 ,过
,过 作射线
作射线 .过顶点
.过顶点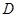 平行于
平行于 轴的直线交射线
轴的直线交射线 于点
于点 ,
, 在
在 轴正半轴上,连结
轴正半轴上,连结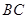 .
.求该抛物线的解析式;
动点
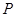 从点
从点 出发,以每秒1个长度单位的速度沿射线
出发,以每秒1个长度单位的速度沿射线 运动,设点
运动,设点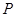 运动的时间为
运动的时间为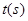 .问当
.问当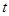 为何值时,四边形
为何值时,四边形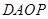 分别为平行四边形?直角梯形?等腰梯形?
分别为平行四边形?直角梯形?等腰梯形?若
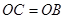 ,动点
,动点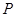 和动点
和动点 分别从点
分别从点 和点
和点 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿
同时出发,分别以每秒1个长度单位和2个长度单位的速度沿 和
和 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为
运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为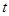
 ,连接
,连接 ,当
,当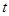 为何值时,四边形
为何值时,四边形 的面积最小?并求出最小值及此时
的面积最小?并求出最小值及此时 的长.
的长.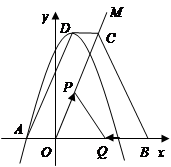
温州市有一种可食用的野生菌,上市时,外商李经理按市场价格30元/千克收购了这种野生菌1000千克存放入冷库中,据预测,该野生菌的市场价格将以每天每千克上涨1元;但冷冻存放这批野生菌时每天需要支出各种费用合计310元,而且这类野生菌在冷库中最多保存160天,同时,平均每天有3千克的野生菌损坏不能出售。设
 天后每千克该野生菌的市场价格为
天后每千克该野生菌的市场价格为 元,试写出
元,试写出 与
与 之间的函数关系式;
之间的函数关系式;若存放
 天后,将这批野生菌一次性出售,设这批野生菌的销售总额为
天后,将这批野生菌一次性出售,设这批野生菌的销售总额为 元,试写出
元,试写出 与
与 之间的函数关系式;
之间的函数关系式;李经理将这批野生菌存放多少天后出售可获得最大利润
 元?
元?
(利润=销售总额-收购成本-各种费用)
在平面直角坐标系xOy中,已知抛物线 与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,
与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N, =
= .
.
(1)求此抛物线的函数表达式;
(2)过H的直线与y轴相交于点P,过O,M两点作直线PH的垂线,垂足分别为E,F,若 =时,求点P的坐标;
(3)将(1)中的抛物线沿y轴折叠,使点A落在点D处,连接MD,Q为(1)中的抛物线上的一点直线NQ交x轴于点G,当Q点在抛物线上运动时,是否存在点Q,使△ANG 与△ADM相似?若存在,求出所有符合条件的直线QG的解析式;若不存在,请说明理由.