2011-2012学年九年级期末模拟测试数学试卷
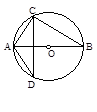
已知⊙O的半径为2cm, 弦AB的长为2 ,则这条弦的中点到弦所对优弧的中点的距离为( )
,则这条弦的中点到弦所对优弧的中点的距离为( )
| A.1cm | B.3cm | C.(2+ )cm )cm |
D.(2+ )cm )cm |
如图,已知A、B、C、D、E均在⊙O上,且AC为直径,则∠A+∠B+∠C=( )度.
A.30 B.45 C.60 D.90
⊿ABC中,∠C=90°,AB=5,BC=4,以A为圆心,以3为半径,则点C与⊙A的位置关系为( )
| A.点C在⊙A内 | B.点C在⊙A上 |
| C.点C在⊙A外 | D.点C在⊙A上或点C在⊙A外 |
设⊙O的半径为r,圆心O到直线L的距离为d,若直线L与⊙O有交点,则d与r的关系为( )
| A.d =r | B.d <r | C.d>r | D.d ≤r |
以点P(1,2)为圆心,r为半径画圆,与坐标轴恰好有三个交点,则r应满足( )
A.r=2或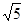 |
B.r=2 | C.r=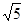 |
D.2≤r≤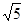 |
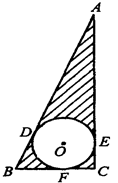
如图中的正方形的边长都相等,其中阴影部分面积相等的图形的个数是( )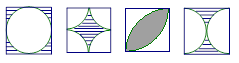
| A.1个 | B.2个 | C.3个 | D.4个 |
两个等圆⊙O1和⊙O2相交于A,B两点,且⊙O1经过点O2,则四边形O1A O2B是( )
| A.两个邻边不相等的平行四边形 | B.菱形 | C.矩形 | D.正方形 |
抛物线y=x2-bx+8的顶点在x轴上,取b的值一定为( ).
| A.4 | B.-4 | C.2或-2 | D.4 或-4 或-4 |
已知二次函数y=ax2+bx+c,且ac<0,则它的图象经过( )
| A.一、二、三象限 | B.二、三、四象限 |
| C.一、三、四象限 | D.一、二、三、四象限 |
要从抛物线y=x2-3得到y=x2的图象,则抛物线y=x2-3必须( ).
| A.向上平移3个单位 | B.向下平移3个单位 |
| C.向左平移3个单位 | D.向右平移3个单位 |
不论x为何值时,y=ax2+bx+c恒为正值的条件是( )
| A.a>0,△>0 | B.a>0,△>0 | C.a>0,△<0 | D.a<0,△<0 |
抛物线y=ax2+bx+c(a )的图象如图所示,则下列四组中正确的是( ).
)的图象如图所示,则下列四组中正确的是( ).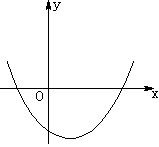
| A.a>0,b>0,c>0 | B.a>0,b<0,c>0 |
| C.a>0,b>0,c<0 | D.a>0,b<0,c<0 |
函数y=2x2+4x+1①;y=2x2- 4x+1②的图象的位置关系是( )
| A.②在①的上方; | B.②在①的下方; | C.②在①的左方; | D.②在①的右方。 |
一组数据共50个,分为6组,第1—4组的频数分别是5,7,8,10,第5组的频率是0.20,则第6组的频数是( )
| A.10 | B.11 | C.12 | D.15 |
已知样本容量为30,在样本分布直方图中各小长方形的高的比依次为2:4:3:1,则第二小组的频数为( )
| A.4 | B.12 | C.9 | D.8 |
在一个暗箱里放入除颜色外其它都相同的3个红球和11个黄球,搅拌均匀后随机任取一个球,取到是红球的概率是( )
A.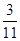 |
B.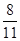 |
C.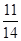 |
D.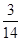 |
有一对酷爱运动的年轻夫妇给他们12个月大的婴儿拼排3块分别写有“20”, “08”和“北京”的字块,如果婴儿能够排成“2008北京”或者“北京2008”,则他们就给婴儿奖励.假设婴儿能将字块横着正排,那么这个婴儿能得到奖励的概率是:
A.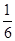 |
B.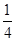 |
C.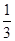 |
D.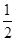 |
如图,已知圆柱体底面圆的半径为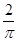 ,高为2,AB、CD分别是两底面的直径,AD、BC是母线,若一只小虫从A点出发,从侧面爬行到C点,则小虫爬行的最短的路线的长度是 (结果保留根式)
,高为2,AB、CD分别是两底面的直径,AD、BC是母线,若一只小虫从A点出发,从侧面爬行到C点,则小虫爬行的最短的路线的长度是 (结果保留根式)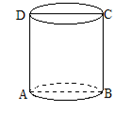
有一个抛物线形桥拱,其最大高度为16米,跨度为40米,现在它的示意图放在平面直角坐标系中(如图),则此抛物线的解析式为 。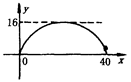
一只袋内装有2个红球、3个白球、5个黄球(这些球除颜色外没有其它区别),从中任意取出一球,则取得红球的概率是___________
某学校为丰富课间自由活动的内容,随机选取本校100名学生进行调查,调查内容是“你最喜欢的自由活动项目是什么”,整理收集到的数据,绘制成直方图,如图所示.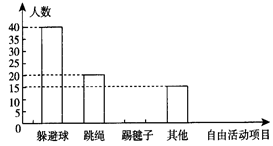
学校采用的调查方式是__________.
求喜欢“踢毽子”的学生人数,并在图中将“踢毽子”部分的图形补充完整;
该校共有800名学生,请估计喜欢“跳绳”的学生人数
已知:如图,AB是⊙O的直径,BC是和⊙O相切于点B的切线,⊙O的弦AD平行于OC.求证:DC是⊙O的切线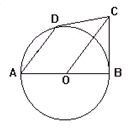
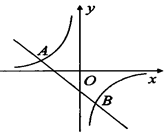
如图,一次函数y=kx+b图象与反比例函数y=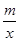 图象交于A(-2,1),B(1,n)两点
图象交于A(-2,1),B(1,n)两点求反比例函数的解析式;
根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
体育测试时,初三一名高个学生推铅球,已知铅球所经过的路线为抛物线 的一部分,根据关系式回答:
的一部分,根据关系式回答: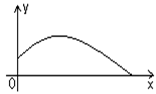
该同学的出手最大高度是多少?
铅球在运行过程中离地面的最大高度是多少?
该同学的成绩是多少?
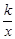 (k≠0), 它们在同一坐标系内的图象大致是( )
(k≠0), 它们在同一坐标系内的图象大致是( )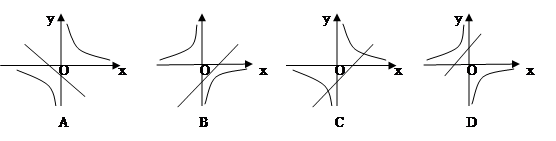
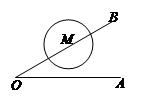
 粤公网安备 44130202000953号
粤公网安备 44130202000953号