初中数学二次函数在给定区间上的最值试题

下列函数中，图象通过原点的是（    ）

A．y=2x+1

B．y=x^2﹣1

C．y=3x^2

D．y=

已知二次函数y=x²+2x-3．
（1）求此二次函数的图象与x轴的交点坐标；
（2）此二次函数的图象经怎样平移，使顶点变为A（3，0），请你描述平移的过程．

在平面直角坐标系中，抛物线C₁:y=ax²－1
（1）若抛物线过点A（1,0），求抛物线C₁的解析式；
（2）将（1）中的抛物线C₁平移，使其顶点在直线L₁：y=x上，得到抛物线C₂，若直线L₁与抛物线C₂交于点C、D，求线段CD的长；
（3）将（1）中的抛物线C₁绕点A旋转180⁰后得到抛物线C₃，直线y=kx－2k＋4与抛物线C₃只有唯一交点，求符合条件的直线l的解析式。

已知抛物线 y=ax²+bx+3 （a≠0） 经过A（5，0）， B（6，1）两点，且与y轴交于点C．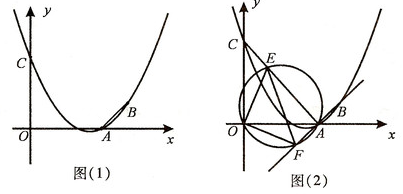

（1）求抛物线y=ax²+bx+3（a≠0）的函数关系式及点C的坐标；
（2）如图（1），连接AB，在题（1）中的抛物线上是否存在点P，使△PAB是以AB为直角边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由；
（3）如图（2），连接AC，E为线段AC上任意一点（不与A重合）经过A、E、O三点的圆交直线AB于点F，求出当△OEF的面积取得最小值时，点E的坐标．

在作二次函数与一次函数的图象时，先列出如下表：

请你根据表格信息回答问题，当＞时，自变量x的取值范围是       ．

阅读材料，解答问题：
若两个二次函数图象的顶点，开口方向都相同，则称这两个二次函数为“同簇二次函数”．
（1）下列各组二次函数中，是“同簇二次函数”的是                （填序号）；
①y=x²+1与y=2x²；
②y=x²+2x+2与y=2（x-1）²+1；
③y=-x²-2x+3与y=-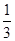（x+1）²+4
（2）已知关于x的二次函数y₁=2x²-4mx+2m²+1和y₂=ax²+bx+5，其中y₁的图象经过点A（1，1），若y₁+y₂与y₁为“同簇二次函数”，求函数y₂的表达式．

下列函数中，是二次函数的是（   ）

A．

B．

C．

D．

二次函数y=a（x-1）²+k（a＞0）中x、y的几组对应值如下表．

x	-2	1	5
y	m	n	p

 
表中m、n、p的大小关系为              （用“＜”连接）

抛物线y=﹣x²+（m﹣1）x+m与y轴交于点（0，3）．
（1）求抛物线的解析式；
（2）求抛物线与坐标轴的交点坐标；
（3）①当x取什么值时，y＞0？②当x取什么值时，y的值随x的增大而减小？

用配方法将二次函数y=x²-2x+1写成y=a（x-h）²+k的形式是（   ）

A．y=（x-2）²-1	B．y=（x-1）²-1
C．y=（x-2）²-3	D．y=（x-1）²-3

二次函数y=x²的图象向上平移2个单位，得到新的图象的二次函数表达式是（    ）

A．y=x^2-2	B．y=（x-2）^2
C．y=x^2+2	D．y=（x+2）^2

关于抛物线y=(x-1)²-2，下列说法中错误的是

A．顶点坐标为(1，-2)

B．对称轴是直线x=1

C．当x＞1时，y随x的增大而减小

D．开口方向向上

二次函数y=-x²+2x+4的最大值为（ ）

A．3

B．4

C．5

D．6

关于二次函数y=（x-1）²+2，则下列说法正确的是（    ）

A．当x=1时，y有最大值为2

B．当x=1时，y有最小值为2

C．当x=-1时，y有最大值为2

D．当x=-1时，y有最小值为2

下列函数中，不属于二次函数的是（    ）

A．y=（x﹣2）^2	B．y=﹣2（x+1）（x﹣1）
C．y=1﹣x﹣x^2	D．y=