浙江省杭州市萧山城区四校九年级上学期期中联考数学试卷
面积为2的△ABC,一边长为x,这边上的高为y,则y与x的变化规律用图象表示大致是( )
A.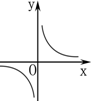 |
B. |
C. |
D. |
在 □4a□4空格□中,任意填上“+”或“-”,在所得到的所有代数式中,能构成完全平方式的概率是( )
□4a□4空格□中,任意填上“+”或“-”,在所得到的所有代数式中,能构成完全平方式的概率是( )
| A.1 | B. |
C. |
D. |
下列命题中,假命题的个数为( )
(1)“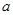 是任意实数,
是任意实数,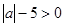 ”是必然事件;
”是必然事件;
(2)抛物线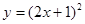 的对称轴是直线
的对称轴是直线 ;
;
(3)若某运动员投篮2次,投中1次,则该运动员投1次篮,投中的概率为 ;
;
(4)某件事情发生的概率是1,则它一定发生;
(5)某彩票的中奖率为10%,则买100张彩票一定有1张会中奖;
(6)函数 与
与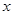 轴必有两个交点.
轴必有两个交点.
| A.2 | B.3 | C.4 | D.5 |
如图,⊙O的直径AB=8,P是圆上任一点(A、B除外),∠APB的平分线交⊙O于C,弦EF 过AC、BC的中点M、N,则EF的长是( )

A. B.
B. C.6 D.
C.6 D.
用列表法画二次函数 的图象时先列一个表,当表中对自变量x的值以相等间隔的值增加时,函数y所对应的值依次为:20、56、110、182、274、380、506、650,其中有一个值不正确,这个不正确的值是( )
的图象时先列一个表,当表中对自变量x的值以相等间隔的值增加时,函数y所对应的值依次为:20、56、110、182、274、380、506、650,其中有一个值不正确,这个不正确的值是( )
| A.506 | B.380 | C.274 | D.182 |
已知二次函数 (
( >0),当自变量
>0),当自变量 取
取 时,其相应的函数值小于0,那么当自变量x取
时,其相应的函数值小于0,那么当自变量x取 时,下列结论中正确的是( )
时,下列结论中正确的是( )
A. 的函数值小于0 的函数值小于0 |
B. 的函数值大于0 的函数值大于0 |
C. 的函数值等于0 的函数值等于0 |
D. 的函数值与0的大小关系不确定 的函数值与0的大小关系不确定 |
关于 的方程
的方程 有两个不相等的实数根,且较小的根为2,则下列结论:
有两个不相等的实数根,且较小的根为2,则下列结论:
① ;②
;② ;③关于
;③关于 的方程
的方程 有两个不相等的实数根;
有两个不相等的实数根;
④抛物线 的顶点在第四象限.其中正确的结论有( )
的顶点在第四象限.其中正确的结论有( )
| A.①② | B.①②③ | C.①②④ | D.①②③④ |
已知函数 (
(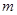 为常数)的图象上有三点:A(
为常数)的图象上有三点:A(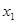 ,
,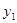 ),B(
),B(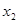 ,
,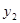 ),C(
),C(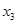 ,
,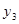 ),其中
),其中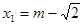 ,
,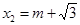 ,
,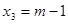 ,则
,则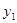 、
、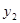 、
、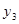 的大小关系是 .
的大小关系是 .
如图是某市9月1日至10日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择9月1日至9月8日中的某一天到达该市,并连续停留3天,则此人在该市停留期间有且仅有1天空气质量优良的概率是 .

一条弦AB把圆的 直径分成3和11两 部分,弦 和 直径相交 成300角,则AB的长为 .
在作二次函数 与一次函数
与一次函数 的图象时,先列出如下表:
的图象时,先列出如下表:

请你根据表格信息回答问题,当 >
> 时,自变量x的取值范围是 .
时,自变量x的取值范围是 .
(本小题满分8分)如图,在⊿ABC中,AB=BC,点D在AB的延长线上.
(1)利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).
①作∠CBD的平分线BM ;
②作边BC上的中线AE,并延长AE交BM于点F;
(2)在(1)的基础上,连接CF,判断四边形ABFC的形状,并说明理由.
(本小题满分8分)甲口袋中装有3个相同的小球,它们分别写有数值﹣1,2,5;乙口袋中装有3个相同的小球,它们分别写有数值﹣4,2,3.现从甲口袋中随机取一球,记它上面的数值为x,再从乙口袋中随机取一球,记它上面的数值为y.设点A的坐标为(x,y).
(1)请用树状图或列表法表示点A的坐标的各种可能情况;
(2)求点A落在 的概率.
的概率.
(本小题满分10分)如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连结ED、BE.
(1)试判断DE与BD是否相等,并说明理由;
(2)如果BC=6,AB=5,求BE的长.
(本小题满分10分)已知关于x的函数 (a为常数).
(a为常数).
(1)若函数的图象与坐标轴恰有两个交点,求a的值;
(2)若函数的图象是抛物线,开口向上且顶点在x轴下方,求a的取值范围.
(本小题满分12分)某商场试销一种成本为每件60元的服装,规定试销期间销售单价不能低于成本单价,且获利不得高于成本的45%,经试销发现,销售量 (件)与销售单价
(件)与销售单价 (元)符合一次函数
(元)符合一次函数 ,且
,且 时,
时, ;
; 时,
时, .
.
(1)求一次函数 的表达式;
的表达式;
(2)若该商场获得利润为 元,试写出利润
元,试写出利润 与销售单价
与销售单价 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价 的范围.
的范围.




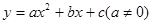 的最大值为0,则( )
的最大值为0,则( )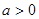 ,
,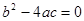
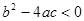
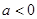 ,
,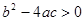
 与
与 的图象,只可能是下图中的( )
的图象,只可能是下图中的( )



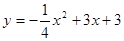 化成
化成 的形式为 .
的形式为 . 的中点,则∠DAC的度数是 .
的中点,则∠DAC的度数是 .
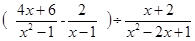 ,其中
,其中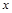 是不等式组
是不等式组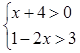 的整数解.
的整数解.
 与x轴交于A ,B两点,且点A在点B的左侧,与y轴交于点C.
与x轴交于A ,B两点,且点A在点B的左侧,与y轴交于点C. 与点Q
与点Q 在(1)中抛物线上,
在(1)中抛物线上, ,
, .求
.求 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号