初中数学二次函数在给定区间上的最值试题

已知二次函数y=ax²＋bx－3的图象经过点A（2，－3），B（－1，0）．求二次函数的解析式

如果将抛物线y＝x²＋2x－1向上平移，使它经过点A（0，3），那么所得新抛物线的表达式是_______________．

如图，二次函数的图象与x轴相交于点（﹣1，0）和（3，0），则它的对称轴是_________．

如图，在直角坐标平面内，直线y=－x+5与轴和轴分别交于A、B两点，二次函数y=+bx+c的图象经过点A、B，且顶点为C．

（1）求这个二次函数的解析式；
（2）求sin∠OCA的值；
（3）若P是这个二次函数图象上位于x轴下方的一点，且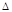ABP的面积为10，求点P的坐标．

已知二次函数
（1）求它的顶点坐标和对称轴；
（2）画出这个函数的图象；
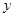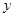（3）根据图象回答：当取哪些值时，＝0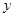，＞0，＜0

二次函数y=3x²的图象向左平移一个单位后函数解析式为（   ）

A．y=3x^2+1

B．y=3x^2﹣1

C．y=3（x﹣1）^2

D．y=3（x+1）^2

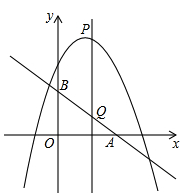
如图，已知直线y=-x+3分别交x轴、y轴于点A、B，P是抛物线y=-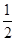x²+2x+5上的一个动点，其横坐标为a，过点P且平行于y轴的直线交直线y=-x+3于点Q，则当PQ=BQ时，a的值是                  ．

已知抛物线-4x+c与x轴只有一个交点，则c=       ．

要将抛物线y=x²+2x+3平移后得到抛物线y=x²，下列平移方法正确的是（ ）

A．向左平移1个单位，再向上平移2个单位

B．向左平移1个单位，再向下平移2个单位

C．向右平移1个单位，再向上平移2个单位

D．向右平移1个单位，再向下平移2个单

抛物线y=3x²，y=-3x²，y=x²+3共有的性质是（    ）

A．开口向上	B．对称轴是y轴
C．都有最高点	D．y随x值的增大而增大

抛物线y=﹣x²+（m﹣1）x+m与y轴交于点（0，3）．
（1）求抛物线的解析式；
（2）求抛物线与坐标轴的交点坐标；
（3）①当x取什么值时，y＞0？②当x取什么值时，y的值随x的增大而减小？

将抛物线y=（x-1）²+3向右平移1个单位，再向上平移3个单位后所得抛物线的表达式为（ ）

A．y=（x-2）^2

B．y=x^2

C．y=x^2+6

D．y=（x-2）^2+6

用配方法将二次函数y=x²-2x+1写成y=a（x-h）²+k的形式是（   ）

A．y=（x-2）²-1	B．y=（x-1）²-1
C．y=（x-2）²-3	D．y=（x-1）²-3

二次函数y=x²的图象向上平移2个单位，得到新的图象的二次函数表达式是（    ）

A．y=x^2-2	B．y=（x-2）^2
C．y=x^2+2	D．y=（x+2）^2

关于抛物线y=(x-1)²-2，下列说法中错误的是

A．顶点坐标为(1，-2)

B．对称轴是直线x=1

C．当x＞1时，y随x的增大而减小

D．开口方向向上