初中数学二次函数在给定区间上的最值试题

二次函数y=a+bx+c（a≠0）的图象如图所示，下列结论正确的是（     ）

A．a＜0

B．－4ac＜0

C．当－1＜x＜3时，y＞0

D．－=1

把二次函数的表达式y=x²－4x+6化为y=a（x－h）²+k的形式，那么h+k=     ．

抛物线y＝2（x－2）²＋3的顶点坐标是 （    ）

A．（－2，3）

B．（2，3）

C．（－1，3）

D．（1，3）

二次函数y=3x²的图象向左平移一个单位后函数解析式为（   ）

A．y=3x^2+1

B．y=3x^2﹣1

C．y=3（x﹣1）^2

D．y=3（x+1）^2

对于抛物线y=ax²+bx+c（a≠0），有下列说法：
①当b=a+c时，则抛物线y=ax²+bx+c一定经过一个定点（-1，0）；
②若△=b²-4ac＞0，则抛物线y=cx²+bx+a与x轴必有两个不同的交点；
③若b=2a+3c，则抛物线y=ax²+bx+c与x轴必有两个不同的交点；
④若a＞0，b＞a+c，则抛物线y=ax²+bx+c与x轴必有两个不同的交点；
其中正确的有               ．

二次函数y＝x²－2x＋3的图像的顶点坐标是

A．（1，2）

B．（1，6）

C．（－1，6）

D．（－1，2）

如果一种变换是将抛物线向右平移2个单位或向上平移1个单位，我们把这种变换称为抛物线的简单变换．已知抛物线经过两次简单变换后的一条抛物线是y=x²+1，则原抛物线的解析式不可能的是（ ）

A．y=x^2-1

B．y=x^2+6x+5

C．y=x^2+4x+4

D．y=x^2+8x+17

如图，已知直线y=-x+3分别交x轴、y轴于点A、B，P是抛物线y=-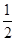x²+2x+5上的一个动点，其横坐标为a，过点P且平行于y轴的直线交直线y=-x+3于点Q，则当PQ=BQ时，a的值是                  ．

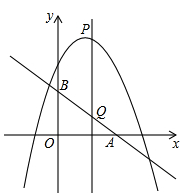
如图，在平面直角坐标系xoy中，矩形ABCD的边AB在x轴上，且AB=3，BC=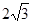，直线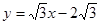经过点C，交y轴于点G．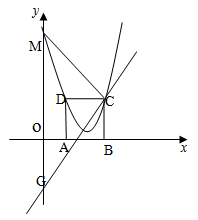

（1）求C,D坐标；
（2）已知抛物线顶点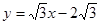上，且经过C，D,若抛物线与y交于点M连接MC,设点Q是线段下方此抛物线上一点，当点Q运动到什么位置时，△MCQ的面积最大？求出此时点Q的坐标和面积的最大值．
（3）将（2）中抛物线沿直线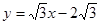平移，平移后的抛物线交y轴于点F，顶点为点E（顶点在y轴右侧）。平移后是否存在这样的抛物线，使⊿EFG为等腰三角形？若存在，请求 出此时抛物线的解析式；若不存在，请说明理由．

已知函数
（1）当时，确定取什么值时，①    ②
（2）解关于的不等式：

抛物线y=﹣x²+（m﹣1）x+m与y轴交于点（0，3）．
（1）求抛物线的解析式；
（2）求抛物线与坐标轴的交点坐标；
（3）①当x取什么值时，y＞0？②当x取什么值时，y的值随x的增大而减小？

用配方法将二次函数y=x²-2x+1写成y=a（x-h）²+k的形式是（   ）

A．y=（x-2）²-1	B．y=（x-1）²-1
C．y=（x-2）²-3	D．y=（x-1）²-3

二次函数y=x²的图象向上平移2个单位，得到新的图象的二次函数表达式是（    ）

A．y=x^2-2	B．y=（x-2）^2
C．y=x^2+2	D．y=（x+2）^2

关于抛物线y=(x-1)²-2，下列说法中错误的是

A．顶点坐标为(1，-2)

B．对称轴是直线x=1

C．当x＞1时，y随x的增大而减小

D．开口方向向上

二次函数y=-x²+2x+4的最大值为（ ）

A．3

B．4

C．5

D．6