初中数学一元二次方程的最值试题

已知a²＋a－3＝0，那么a²(a＋4)的值是

A．9

B．－12

C．－18

D．－15

某楼盘准备以每平方米6000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米4860元的均价开盘销售。
（1）求平均每次下调的百分率。
（2）某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，一次性送装修费每平方米80元。
试问哪种方案更优惠？

某公司实行年工资制，职工的年工资由基础工资、住房补贴和医疗费三项组成，具体规定如下：

项目	第一年的工资（万元）	一年后的计算方法
基础工资	1	每年的增长率相同
住房补贴	0.04	每年增加0.04
医疗费	0.1384	固定不变

 
设基础工资每年的增长率为，用含的代数式表示第三年的基础工资为  万元.
某人在公司工作了3年，他算了一下这3年拿到的住房补贴和医疗费正好是这3年基础工资总额的18%，问基础工资每年的增长率是多少？

在锐角△ABC中，AB＝AC，∠A使关于x的方程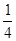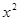－sinA x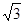＋sinA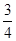－＝0有两个相等的实数根.
判断△ABC的形状；
设D为BC上的一点，且DE⊥AB于E，DF⊥AC于F，若DE＝m，DF＝n，且3m＝4n和m²＋n²＝25，求AB的长.

若满足，则的值           ．

已知，在矩形ABCD中，AB=a，BC=b，动点M从点A出发沿边AD向点D运动．
（1）如图1，当b=2a，点M运动到边AD的中点时，请证明∠BMC=90°；
（2）如图2，当b＞2a时，点M在运动的过程中，是否存在∠BMC=90°，若存在，请给与证明；若不存在，请说明理由；
（3）如图3，当b＜2a时，（2）中的结论是否仍然成立？请说明理由．

某农场去年种植了10亩地的南瓜，亩产量为2000千克，根据时常需要，今年该农场扩大了种植面积，并且全部种植了高产的新品种南瓜，已知南瓜的种植面积的增长率是亩产量的增长率的2倍，今年南瓜的总产量为60000千克，求南瓜亩产量的增长率。

有一人患了流感，经过两轮传染后共有81人患了流感，每轮传染中平均一个人传染了几个人？

（本题12分）已知，如图，在平面直角坐标系中，点A、B的横坐标恰好是方程的解，点C的纵坐标恰好是方程的解，点P从C点出发沿y轴正方向以1个单位/秒的速度向上运动，连PA、PB，D为AC的中点.

1）求直线BC的解析式；
2）设点P运动的时间为t秒，问：当t为何值时，DP与DB垂直且相等？
3）如图2，若PA=AB，在第一象限内有一动点Q，连QA、QB、QP，且∠PQA=60°，问：当Q在第一象限内运动时，∠APQ+∠ABQ的度数和是否会发生改变？若不变，请说明理由并求其值.

为建设美丽家园，某企业逐年增加对环境保护的经费投入，2012年投入了400万元，预计到2014年将投入576万元．
（1）求2012年至2014年该单位环保经费投入的年平均增长率；
（2）该单位预计2015年投入环保经费不低于680万元，若继续保持前两年的年平均增长率，该目标能否实现？请通过计算说明理由．

我县某楼盘准备以每平方米4000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米3240元的均价开盘销售．
（1）求平均每次下调的百分率．
（2）某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：①打9．8折销售；②不打折，一次性送装修费每平方米80元，试问哪种方案更优惠？

解方程
（1）x²－10x=96 
（2）阅读下面的例题：
解方程x²-|x|－2=0．                       
解：分两种情况讨论：
①当x≥0时，原方程化为x²－x－2=0．
解得：x₁=2，x₂=－1(不合题意，舍去)；
②当x＜0时，原方程化为x²＋x－2=0．
解得：x₁=－2，x₂=1(不合题意，舍去)；
综上所述，原方程的根是x₁=2，x₂=－2．
请参照前面的例题的解法解方程：x²-|x－1|－1=0

随着人们环保意识的不断增强，我市家庭电动自行车的拥有量逐年增加．据统计，某小区2009年底拥有家庭电动自行车125辆，2011年底家庭电动自行车的拥有量达到180辆．
（1）若该小区2009年底到2012年底家庭电动自行车拥有量的年平均增长率相同，则该小区到2012年底电动自行车将达到多少辆？
（2）为了缓解停车矛盾，该小区决定投资3万元再建若干个停车位，据测算，建造费用分别为室内车位1000元/个，露天车位200元/个．考虑到实际因素，计划露天车位的数量不少于室内车位的2倍，但不超过室内车位的2.5倍，则该小区最多可建两种车位各多少个？试写出所有可能的方案．

某百货大搂服装柜在销售中发现：“七彩”牌童装平均每天可售出20件，每件盈利40元．为了迎接“元旦”，商场决定采取适当的降价措施，扩大销售量，增加盈利，减少库存．经市场调查发现：如果每件童装降价1元，那么平均每天就可多售出2件．
（1）要想平均每天销售这种童装盈利1200元，那么每件童装应降价多少元？
（2）用配方法说明：要想盈利最多，每件童装应降价多少元？

若关于x的方程有实数解，则实数a的取值范围是          ．