江苏省大丰市刘庄镇三圩初中九年级上学期第一次月考数学试卷
一元二次方程x2-x+4="0" 的根的情况为( )
| A.有两个不相等的实数根 |
| B.有两个相等的实数根 |
| C.只有一个实数根 |
| D.没有实数根 |
关于x的方程3x2-2x+m=0的一个根是﹣1,则m的值为( ).
| A.5 | B.﹣5 | C.1 | D.﹣1 |
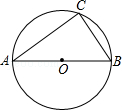
如图,AB是⊙O直径,∠AOC=110°,则∠D=( )

| A.65° | B.25° | C.15° | D.35° |
在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙A的半径为2,下列说
法中不正确的是( )
| A.当1<a<5时,点B在⊙A内 |
| B.当a<5时,点B在⊙A内 |
| C.当a<1时,点B在⊙A外 |
| D.当a>5时,点B在⊙A外 |
如图,在平面直角坐标系中,点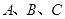 的坐标为(1,4)、(5,4)、(1、
的坐标为(1,4)、(5,4)、(1、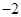 ),则
),则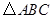 外接圆的圆心坐标是( )
外接圆的圆心坐标是( )
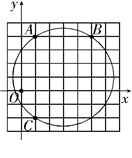
| A.(3,1) | B.(3,2) | C.(1,3) | D.(2,3) |
下列四个命题:
①弦是直径;
②经过三个点一定可以作圆;
③三角形的外心到三角形各顶点的距离都相等;
④半径相等的两个半圆是等弧.
其中正确的有( )
| A.4个 | B.3个 | C.2个 | D.1个 |
在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx﹣3k+4与
⊙O交于B、C两点,则弦BC的长的最小值为( )

A.22 B.24 C. D.
D.
如图,C是以AB为直径的⊙O上一点,已知AB=5,BC=3,则圆心O到弦BC的距离是 .
要组织一次篮球联赛,赛制为单循环形式(每两队之间都比赛一场),计划安排15场比赛,应邀请多少个球队参加比赛?设有 个球队参赛,列出正确的方程___________________.
个球队参赛,列出正确的方程___________________.
若正数a是一元二次方程x2﹣5x+m=0的一个根,﹣a是一元二次方程x2+5x﹣m=0的一个根,则a的值是 .
已知一元二次方程x2-4x+k=0有两个不相等的实数根
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2-4x+k=0与x2+mx-1=0有一个相同的根,求此时m的值.
大丰区为打造“绿色城市”,积极投入资金进行河道治污与园林绿化两项工程,已知2013年投资1000万元,预计2015年投资1210万元.若这两年内平均每年投资增长的百分率相同.
(1)求平均每年投资增长的百分率;
(2)按此增长率,计算2016年投资额能否达到1360万?
如图所示,AB是圆O的直径,以OA为直径的圆C与圆O的弦AD相交于点E.
求证:点E为AD的中点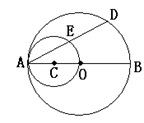
在等腰△ABC中,三边分别为 、
、 、
、 ,其中
,其中 ,若关于
,若关于 的方程、
的方程、 有两个相等的实数根,求△
有两个相等的实数根,求△ 的周长.
的周长.
每位同学都能感受到日出时美丽的景色.右图是一位同学从照片上剪切下来的画面,“图上”太阳与海平线交于A﹑B两点,他测得“图上”圆的半径为5厘米,AB=8厘米,若从目前太阳所处位置到太阳完全跳出海面的时间为16分钟,求“图上”太阳升起的速度.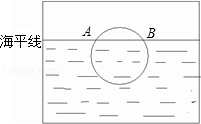
如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB=24cm,CD=8cm.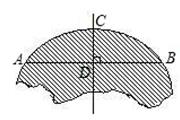
(1)求作此残片所在的圆(不写作法,保留作图痕迹)
(2)求残片所在圆的面积
悦达汽车4S店“十一”黄金周销售某种型号汽车,该型号汽车的进价为30万元/辆,若黄金周期间销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,黄金周期间销售量不会突破30台.已知该型号汽车的销售价为32万元/辆,悦达汽车4S店计划黄金周期间销售利润25万元,那么需售出多少辆汽车?(注:销售利润=销售价﹣进价)
已知:如图,等边△ABC内接于⊙O,点P是劣弧 上的一点(端点除外),延长BP至D,使BD=AP,连接CD.
上的一点(端点除外),延长BP至D,使BD=AP,连接CD.
(1)若AP过圆心O,如图①,请你判断△PDC是什么三角形?并说明理由;
(2)若AP不过圆心O,如图②,△PDC又是什么三角形?为什么?
阅读下列材料,然后解答问题.
经过正四边形(即正方形)各顶点的圆叫做这个正四边形的外接圆,圆心是正四边形的对称中心,这个正四边形叫做这个圆的内接正四边形.
如图,正方形ABCD内接于⊙O,⊙O的面积为S1,正方形ABCD的面积为S2.以圆心O为顶点作∠MON,使∠MON=90°.将∠MON绕点O旋转,OM、ON分别与⊙O交于点E、F,分别与正方形ABCD的边交于点G、H.设由OE、OF、 及正方形ABCD的边围成的图形(阴影部分)的面积为S.
及正方形ABCD的边围成的图形(阴影部分)的面积为S.
(1)当OM经过点A时(如图①),则S、S1、S2之间的关系为: (用含S1、S2的代数式表示);
(2)当OM⊥AB于G时(如图②),则(1)中的结论仍然成立吗?请说明理由;
(3)当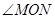 旋转到任意位置时(如图③),则(1)中的结论仍然成立吗?请说明理由;
旋转到任意位置时(如图③),则(1)中的结论仍然成立吗?请说明理由;

 的一元二次方程是( ).
的一元二次方程是( ).



 的解为 .
的解为 . 的两个实数根,该三角形的面积为 .
的两个实数根,该三角形的面积为 .
 有实数解,则实数a的取值范围是 .
有实数解,则实数a的取值范围是 . ”,其规则为
”,其规则为 ,根据这个规则,方程
,根据这个规则,方程 的解为 .
的解为 .
 粤公网安备 44130202000953号
粤公网安备 44130202000953号