江苏省苏州市高新区七年级下学期期末考试数学试题
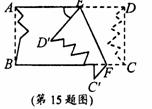
如图,在Rt△ABC中,∠ACB=90°,AC=BC,以AC为直径作QO,OB交QO于E,AE的延长线交BC于D,连结CE.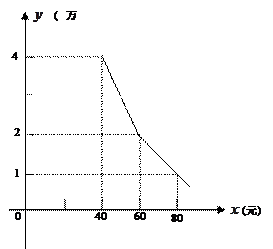
(1)求证△BED~△BCE.
(2)若AC=4,求CD的长.
为了扶持大学生自主创业,市政府提供了80万元的无息贷款,用于某大学生开办公司并销售自研发的的一种电子产品,并约定用该公司经营利润逐步偿还无息贷款。已知该产品的生产成本为每件40元,员工每人每月工资为2500元,公司每月需支付其它费用15万元,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示。
(1) 求月销售量(万件)与销售单价x(元)之间的函数关系式;
(2) 当销售单价定为50元时,为保证公司月利润达到5万元(利润=销售额-生产成本-员工工资-其它费用),该公司可安排员工多少人?
(3) 若该公司有80名员工,则该公司最早可以几个月后还清无息贷款?
在等腰Rt△ABC中,AB=BC点E在BC上,以AE为边作正方形AEMN,EM交AB于F,连结BM.
(1)求证:BM⊥AB
(2)若CE=2BE,求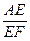 的值.
的值.
 |
在平面直角坐标系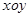 中,已知二次函数
中,已知二次函数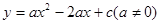 的图象与x轴交于A,B两点(点A在点B的左边),AB=4,与y轴交于点C,且过点(2,3).
的图象与x轴交于A,B两点(点A在点B的左边),AB=4,与y轴交于点C,且过点(2,3).
(1)求此二次函数的表达式;
(2)若抛物线的顶点为D,连接CD、CB,问抛物线上是否存在点P,使得∠PBC+∠BDC=90°. 若存在,求出点P的坐标;若不存在,请说明理由; (3)点K抛物线上C关于对称轴的对称点,点G抛物线上的动点,在x轴上是否存在点F,使A、K、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由
(3)点K抛物线上C关于对称轴的对称点,点G抛物线上的动点,在x轴上是否存在点F,使A、K、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由
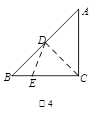
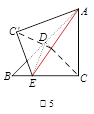
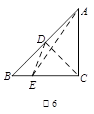
下列图案给出了折叠一个直角边长为2的等腰直角三角形纸片(图1)的全过程:首先对折,如图2,折痕CD交AB于点D;打开后,过点D任意折叠,使折痕DE交BC于点E,如图3;打开后,如图4;再沿AE折叠,如图5;打开后,折痕如图6.则折痕DE和AE长度的和的最小值是


A.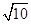 |
B.1+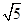 |
C.2 |
D.3 |
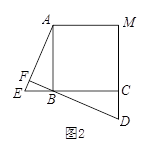
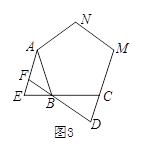
如图,点E、D分别是正三角形ABC、正四边形ABCM、正五边形ABCMN中以C点为顶点的一边延长线和另一边反向延长线上的点,且BE=CD,DB的延长线交AE于点F,则图1中∠AFB的度数为 ;若将条件“正三角形、正四边形、正五边形”改为“正n边形”,其他条件不变,则∠AFB的度数为 .(用n的代数式表示,其中,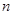 ≥3,且
≥3,且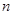 为整数)
为整数)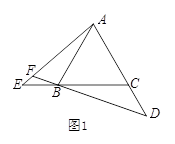
列方程(组)解应用题
某服装厂接到加工720件衣服的订单,原计划每天做48件,即可顺利交货.但还没开工,又接到客户提前5天交货的要求,所以,每天必需多加工几件衣服才能按时交货.问每天应比原计划多加工多少件衣服?
如图,已知点C在⊙O上,延长直径AB到点P,连接PC,∠COB=2∠PCB.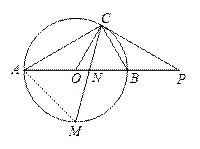
(1)求证:PC是⊙O的切线;
(2)若AC=PC,且PB=3,M是⊙O下半圆弧的中点,求MA的长.
某中学开展了一次“诚信做人”的主题演讲比赛.赛程共分“预赛、复赛和决赛”三个阶段,预赛由各班举行,全员参加,按统一标准评分.统计后制成“预赛成绩统计图(未画完整)”,从预赛中各年级产生 名选手进行复赛,成绩见“复赛成绩统计表”.(采用
名选手进行复赛,成绩见“复赛成绩统计表”.(采用 分制,得分都为
分制,得分都为 分以上的整数.)
分以上的整数.)
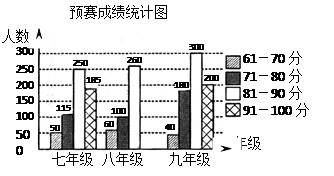 |
||
 |
(1)如果将九年级预赛成绩制成扇形统计图,则“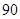 分以上的人数”对应的圆心角度数是___________.
分以上的人数”对应的圆心角度数是___________.
(2)如果八年级复赛成绩在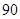 分以上的人数是预赛时同类成绩人数的
分以上的人数是预赛时同类成绩人数的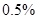 ,请补全预赛成绩统计图.
,请补全预赛成绩统计图.
(3)复赛成绩中,七年级选手的成绩的中位数是___________;九年级选手的成绩的众数是 .
如图,一个横截面为Rt△ABC的物体,∠ACB=90°,∠CAB=30°,BC=1米,师傅要把此物体搬到墙边,先将AB边放在地面(直线m上),再按顺时针方向绕点B翻转到△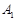 B
B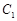 的位置(B
的位置(B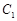 在m上),最后沿射线B
在m上),最后沿射线B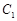 的方向平移到△
的方向平移到△
 的位置,其平移距离为线段AC的长度(此时,
的位置,其平移距离为线段AC的长度(此时,
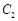 恰好靠在墙边).
恰好靠在墙边).
(1)直接写出AB、AC的长;
(2)画出在搬动此物体的整个过程中A点所经过的路径,
并求出该路径的长度.
如图,在△ABC中,BC=3,AC=2,P为BC边上一个动点,过点P作PD∥AB,交AC于点D,连结BD.
(1)如图1,若∠C=45°,请直接写出:当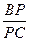 = 时,
= 时,
△BDP的面积最大; (2)如图2,若∠C=α为任意锐角,则当点P在BC上何处时,
(2)如图2,若∠C=α为任意锐角,则当点P在BC上何处时,
△BDP的面积最大?
现场学习:我们知道,若锐角α的三角函数值为sinα= m,则可通过计算器得到角α的大小,这时我们用arc sin m来表示α,记作:α="arc" sin m;若cos α = m,则记α=" arc" cos m;若tan α= m,则记α=" arc" tan m.
解决问题:如图,已知正方形ABCD,点E是边AB上一动点,点F在AB边或其延长线上,点G在边AD上.连结ED,FG,交点为H.
(1)如图1,若AE=BF=GD,请直接写出∠EHF= °;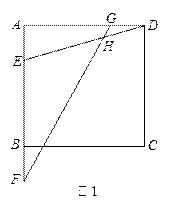 (2)如图2,若EF=
(2)如图2,若EF=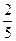 CD,GD=
CD,GD=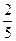 AE,设∠EHF=α.请判断当点E在AB上运动时, ∠EHF的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请求出α.
AE,设∠EHF=α.请判断当点E在AB上运动时, ∠EHF的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请求出α.
下列各式从左边到右边的变形是因式分解的是( )
| A.(a+1)(a-1)=a2-1 | B.a2-6a+9=(a-3)2 |
| C.x2+2x+1=x(x+2x)+1 | D.-18x4y3=-6x2y2·3x2y |
如图所示,两条直线AB、CD被第二条直线EF所截,∠1=75°,
则下列条件,能使AB∥CD的是( )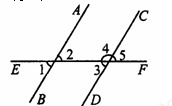
A.∠2=75°
B.∠4=75°
C.∠3=105°
D.∠5=75°
为了了解某地区初一年级5000名学生的体重情况,从中抽取了450名学生的体重,
就这个问题来说,下面说法中正确的是( )
| A.样本容量是450 | B.每个学生是个体 |
| C.450名学生是所抽取的一个样本 | D.5000名学生是总体 |
如图是长10cm,宽6cm的长方形,在四个角剪去4个边长为x cm的小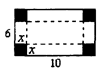 正方形,按折痕做一个有底无盖的长方体盒子,这个盒子的容积是
正方形,按折痕做一个有底无盖的长方体盒子,这个盒子的容积是
| A.(6-2x)(10-2x) | B.x(6-x)(10-x) |
| C.x(6-2x)(10-2x) | D.x(6-2x)(10-x) |
如图,小章利用一张左、右两边已经破损的长方形纸片ABCD做折纸游戏,他将纸片沿E F折叠后,D、C两点分别落在D'、C'的位置,并利用量角器量得∠EFB=65°,则∠AED'等于 度.
F折叠后,D、C两点分别落在D'、C'的位置,并利用量角器量得∠EFB=65°,则∠AED'等于 度.
某初级中学为了解学生的身高状况,在1500名学生中抽取部分学生进行抽样统计,结果如下:
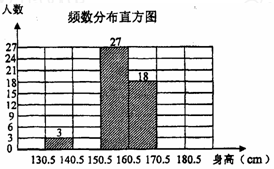
请你根据上面的图表,解答下列问题:
(1)此次抽样调查中样本容量为 ;
(2)m= ,n= ;
(3)补全频数分布直方图;
(4)请你估计该校1500名学生中身高处于160.5~170.5cm的人数约为 人.
如图,已知∠AOB=120°,OM平分∠AOB,将正三角形的一个顶点P放在射
线OM上,两边分别与OA、OB交于点C、D.
(1)如图①若边PC和OA垂直,那么线段PC和PD相等吗?为什么?
(2)如图②将正三角形绕P点转过一角度,设两边与OA、OB分别交于C',D',那么线段PC'
和PD'相等吗?为什么?
某体育彩票经销商计划用45000元从省体彩中心购进彩票20扎,每扎1 0 00张,
00张,
已知体彩中心有A、B、C三种不同价格的彩票,进价分别是A彩票每张1.5元, B彩票每
B彩票每
张2元,C彩票每张2.5元.
(1)若经销商同时购进两种不同型号的彩票20扎,并将45000元恰好用完,请你帮助经销商
设计进票方案:
(2)若销售A型彩票一张获手续费0.2元,B型彩票一张获手续费0.3元,C型彩票一张获手续费0.5元.在问题(1)设计的购进两种彩票的方案中,为使销售完时获得的手续费最多,你选择哪种进票方案?
(3)若经销商准备用45 000元同时购进A、B、C三种彩票20扎,请你帮助经销商设计一种
进票方案.(直接写出答案)
 2的绝对值是
2的绝对值是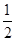

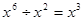

 D,CE交AB于点F,∠DCF
D,CE交AB于点F,∠DCF =110°,且AE=AF,则∠A等于
=110°,且AE=AF,则∠A等于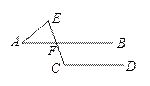
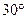 B.
B.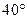 C
C .
.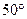 D.
D.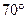
 ,则它的边数是
,则它的边数是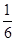
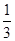
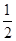
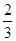
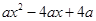 分解因式,下列结果中正确的是
分解因式,下列结果中正确的是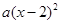


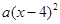

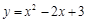 化为
化为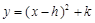 的形式,结果为
的形式,结果为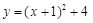

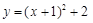

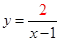 中,自变量
中,自变量 的取值范围是 .
的取值范围是 . 中,
中, 分别是
分别是 和
和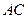 的中点,
的中点, 是
是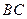 延长线上一点,
延长线上一点,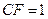 ,
,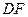 交
交 于点
于点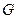 ,且EG=CG,则
,且EG=CG,则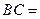 .
.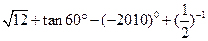 .
.
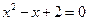 ,求(
,求(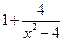 )
) (x+2)的值.
(x+2)的值.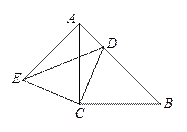 D为AB边上一点.求证: AE=BD.
D为AB边上一点.求证: AE=BD. 经过点
经过点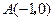 和点
和点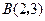 ,另一条直线
,另一条直线

 ,且与
,且与 轴相交于点
轴相交于点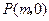 .
. 的面积为3,求
的面积为3,求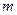 的值.
的值.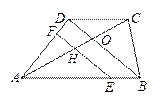

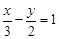 的一个解,则a= .
的一个解,则a= .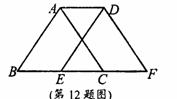


 °
°

 =
= ,b=-
,b=-
 的解适
的解适 合x+y=2,求m的值.
合x+y=2,求m的值. (1)求证:△ABC≌△CDE;
(1)求证:△ABC≌△CDE; +y2-3xy=4.求下列各式的值:
+y2-3xy=4.求下列各式的值: 秒后,△AEP与△BPQ是否全等,请说明理由,并判断此时线段PE和线段PQ的位置关系;
秒后,△AEP与△BPQ是否全等,请说明理由,并判断此时线段PE和线段PQ的位置关系;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号