初中数学应用类问题试题

某化妆品公司每月付给销售人员的工资有两种方案．
方案一：没有底薪，只拿销售提成；方案二：底薪加销售提成．
设x（件）是销售商品的数量，y（元）是销售人员的月工资．如图所示，y1为方案一的函数图象，y2为方案二的函数图象．已知每件商品的销售提成方案二比方案一少7元．从图中信息解答如下问题
（注：销售提成是指从销售每件商品得到的销售额中提取一定数量的费用）：

（1）求y1的函数解析式；
（2）请问方案二中每月付给销售人员的底薪是多少元？
（3）如果该公司销售人员小丽的月工资要超过1000元，那么小丽选用哪种方案最好？至少要销售商品多少件？

下面两个多位数1248624……、6248624……，都是按照如下方法得到的：将第一位数字乘以2，若积为一位数，将其写在第2位上，若积为两位数，则将其个位数字写在第2位。对第2位数字再进行如上操作得到第3位数字……，后面的每一位数字都是由前一位数字进行如上操作得到的。当第1位数字是3时，仍按如上操作得到一个多位数，则这个多位数前100位的所有数字之和是（   ）

A． 495

B． 497

C． 501

D．503

若某人沿坡度i＝1:3的斜坡前进20米,则他所在的位置比原来的位置高__

观察下列关系式:…,设表示正数,用关于的等式表示这个规律为:            

用表示三种不同的物体，现放在天平上比较两次，情况如图所示，那么这三种物体按质量从大到小的顺序排列应为（   ）

      

某校欲招聘一名数学教师，学校对甲、乙、丙三位候选人进行了三项能力测试，各项测试成绩满分均为100分，根据结果择优录用．三位候选人的各项测试成绩如下表所示：

测试项目	测试成绩
甲	乙	丙
教学能力	85	73	73
科研能力	70	71	65
组织能力	64	72	84

 
（1）如果根据三项测试的平均成绩，谁将被录用，说明理由；
（2）根据实际需要，学校将教学、科研和组织三项能力测试得分按5∶3∶2的比例确定每人的成绩，谁将被录用，说明理由

如图，为了测量池塘的宽度DE，在池塘周围的平地上选择了A、B、C三点，且A、D、E、C四点在同一条直线上，∠C=90°，已测得AB=100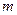，BC=60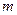，AD=20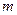，EC=10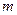，求池塘的宽度DE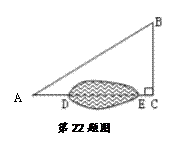

如图1，已知直线的解析式为,它与轴、y轴分别相交于A、B两点．点C从点O出发沿OA以每秒1个单位的速度向点A匀速运动；点D从点A出发沿AB以每秒1个单位长的速度向点B匀速运动，点C、D同时出发，当点C到达点A时同时停止运动．伴随着C、D的运动，EF始终保持垂直平分CD，垂足为E，且EF交折线AB-BO-AO于点F．

(1)直接写出A、B两点的坐标；
(2) 设点C、D的运动时间是t秒（t＞0）．
①用含t的代数式分别表示线段AD和AC的长度；
②在点F运动的过程中，四边形BDEF能否成为直角梯形？若能求t的值；若不能，请说明理由．(可利用备用图解题)

如图，一架2.5米长的梯子,斜靠在一竖直的墙上,这时梯足到墙底端的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯足将向外移多少米?

在平静的湖面上，有一支红莲，高出水面1米，阵风吹来，红莲被吹到一边，
花朵齐及水面，已知红莲移动的水平距离为2米，问这里水深是（    ）

A． 1米

B． 1.5米

C． 2米

D． 2.5米

如图，已知一架竹梯AB斜靠在墙角MON处，竹梯AB=13m，梯子底端离墙角的距离BO=5m．

（1）求这个梯子顶端A距地面有多高；
（2）如果梯子的顶端A下滑4 m到点C，那么梯子的底部B在水平方向上滑动的距离
BD="4" m吗？为什么？

甲种蔬菜保鲜适宜的温度是1℃~5℃，乙种蔬菜保鲜适宜的温度是3℃~8℃，将这两种蔬菜放在一起同时保鲜，适宜的温度是（    ）

A．1℃~3℃

B．3℃~5℃

C．5℃~8℃

D．1℃~8℃

(本题满分9分)
刘卫同学在一次课外活动中，用硬纸片做了两个直角三角形，见图①、②．图①中，，，；图②中，，，．图③是刘卫同学所做的一个实验：他将的直角边与的斜边重合在一起，并将沿方向移动．在移动过程中，、两点始终在边上(移动开始时点与点重合)．
(1)在沿方向移动的过程中，刘卫同学发现：、两点间的距离逐渐 ▲ ．
(填“不变”、“变大”或“变小”)
(2)刘卫同学经过进一步地研究，编制了如下问题：
问题①：当移动至什么位置，即的长为多少时，、的连线与平行?
问题②：当移动至什么位置，即的长为多少时，以线段、、的长度为三边长的三角形是直角三角形?
问题③：在的移动过程中，是否存在某个位置，使得?如果存在，
求出的长度；如果不存在，请说明理由．
请你分别完成上述三个问题的解答过程．

如图，在4×4的方格纸中(共有16个小方格)，每个小方格都是边长为1的正方形． 、、分别是小正方形的顶点，则扇形的弧长等于 ▲ ．(结果保留根号及)．

庞亮和李强相约周六去登山，庞亮从北坡山脚C处出发，以24米/分钟的速度攀登，同时，李强从南坡山脚B处出发．如图，已知小山北坡的坡度，山坡长为240米，南坡的坡角是45°．问李强以什么速度攀登才能和庞亮同时到达山顶A？（将山路AB、AC看成线段，结果保留根号）