初中数学应用类问题试题

将图1中的正方形剪开得到图2，图2 中共有4个正方形；将图2中一个正方形剪开得到图3，图3中共有7个正方形；将图3中一个正方形剪开得到图4，图4中共有10个正方形；……； 如此下去．则图10中正方形的个数是 (   )

A．28

B．29

C．31

D．32

为促进“平安重庆”建设，市公安局交巡警总队拟在我市某“三角形”转盘区域内新增一个交巡警平 台，使交巡警平台到三个十字路 a 的距离相等，试确定交巡警平台 P的位置．(要求：用尺规作图， 保留作图痕迹，不写已知、求作和作法)．

用边长为1的正方形做了一套七巧板，拼成如图1所示的一座桥，则桥中阴影部分的面积为原正方形面积的（   ）

A．

B．

C．

D．不能确定

如图所示，是我们常用的一副三角板．请你用一副三角板画出度数分别为15°和135°的两个角．（要求：保留画图痕迹）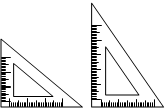

（2）
在下面的方格纸中经过点C画与线段AB互相平行 的直线l1，再经过点B画一条与线段AB垂直的直线l2．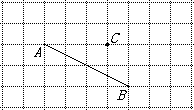

如图是图形的操作过程（四个矩形水平方向的边长均为a，竖立方向的边长均为b）：将线段A₁A₂向右平移1个单位得到B₁B₂，得到封闭图形A₁A₂B₂B₁[即阴影部分如图（1）]；将折线A₁A₂A₃向右平移1个单位得到B₁B₂B₃，得到封闭图形A₁A₂A₃B₃B₂B₁[即阴影部分如图（2）].
（1）在图（3）中，请你类似地画出一条有两个折点的直线，同样向右平移1个单位，从而得到1个封闭图形，并画出阴影.
（2）请你分别写出上述三个阴影部分外的面积S₁=        ，S₂=       ，S₃=        .
（3）联想与探索：如图（4），在一矩形草地上，有一条弯曲的柏油小路（小路任何地方的水平宽度都是1个单位）.请你猜想空白部分草地面积是多少？

 

如果一个点能与另外两个点能构成直角三角形，则称这个点为另外两个点的勾股点．例如：矩形ABCD中，点C与A，B两点可构成直角三角形ABC，则称点C为A，B两点的勾股点．同样，点D也是A，B两点的勾股点．

（1）如图1，矩形ABCD中，AB＝2，BC＝1，请在边CD上作出A，B两点的勾股点（点C和点D除外）（要求：尺规作图，保留作图痕迹，不要求写作法）；
（2）矩形ABCD中，AB＝3，BC＝1，直接写出边CD上A， B两点的勾股点的个数；
（3）如图2，矩形ABCD中，AB＝12，BC＝4，DP=4，DM＝8，AN＝5．过点P作直线l平行于BC，点H为M，N两点的勾股点，且点H在直线l上．求PH的长．

如图所示,是用一张长方形纸条折成的。如果∠1=100°,那么∠2=        °.

如图，零件的外径为16cm，要求它的壁厚x，需要先求出内径AB，现用一个交叉钳(AD与BC相等)去量，若测得OA︰OD=OB︰OC=3︰1，CD＝5cm，你能求零件的壁厚x吗？

如图，AB是⊙O的弦，半径OA=2，∠AOB=120°，则弦AB的长是（    ）

A．

B．2

C．

D．

小颖按如图所示的程序输入一个正数x，最后输出的结果为656，则满足条件的x的不同值最多有   ▲   个．

如图4，王华晚上由路灯A下的B处走到Ｃ处时，测得影子CD的长为１米，继续往前走３米到达Ｅ处时，测得影子EF的长为2米，已知王华的身高是1.5米，那么路灯A的高度AB等于

A．4.5米

B．6米

C．7.2米

D．8米

如图，某同学在测量建筑物AB的高度时，在地面的C处测得点A的仰角为30°，向前走60米到达D处，在D处测得点A的仰角为45°，求建筑物AB的高度.

如图，一个直径为8cm的杯子，在它的正中间竖直放一根筷子，筷子露出杯子外1cm，当筷子倒向杯壁时（筷子底端不动），筷子顶端刚好触到杯口，求筷子长度和杯子的高度。

某校九年级数学兴趣小组的同学开展了测量湘江宽度的活动．
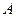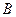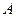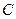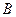如图，他们在河东岸边的点测得河西岸边的标志物在它的正西方向，然后从点出发沿河岸向正北方向行进550米到点处，测得在点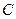的南偏西60°方向上，他们测得的湘江宽度是多少米？

（结果保留整数，参考数据：，）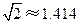

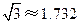如图，AC是电杆AB的一根拉线，测得BC=6米，∠ACB=52°，则拉线AC的长为

A．米

B．米

C．6·cos52°米

D．米