初中数学应用类问题试题

如图，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm．点D，E，F分别是边AB，BC，AC的中点，连接DE、DF，动点P，Q分别从点A、B同时出发，运动速度均为1cm/s，点P沿AFD的方向运动到点D停止；点Q沿BC的方向运动，当点P停止运动时，点Q也停止运动．在运动过程中，过点Q作BC的垂线交AB于点M，以点P，M，Q为顶点作平行四边形PMQN．设平行四边形边形PMQN与矩形FDEC重叠部分的面积为y（cm²）（这里规定线段是面积为0的几何图形），点P运动的时间为x（s）

（1）当点P运动到点F时，CQ=　 　cm；
（2）在点P从点F运动到点D的过程中，某一时刻，点P落在MQ上，求此时BQ的长度；
（3）当点P在线段FD上运动时，求y与x之间的函数关系式．

用半径为10cm，圆心角为216°的扇形做成一个圆锥的侧面，则这个圆锥的高为　   　cm．

图为手的示意图，在各个手指间标记A,B,C,D请你按图中箭头所指方向（A→B→C→D→C→B→A→B→C→ 的方式），从A开始数连续正整数1,2,3,4 当数到2011时，其对应的字母是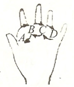

A．A

B．B

C． C

D．D

如图，在平面内，两条直线l₁，l₂相交于点O，对于平面内任意一点M，若p，q分别是点M到直线l₁，l₂，的距离，则称（p，q）为点M的“距离坐标”．根据上述规定，“距离坐标”是（3,2）的点共有             个．

如图，在△ABC中，AD是BC边上的中线，如果，，那么       （用，表示）．

一种电讯信号转发装置的发射直径为31km．现要求：在一边长为30km的正方形城区选择若干个安装点，每个点安装一个这种转发装置，使这些装置转发的信号能完全覆盖这个城市．问：
（1）能否找到这样的4个安装点，使得这些点安装了这种转发装置后能达到预设的要求？
（2）至少需要选择多少个安装点，才能使这些点安装了这种转发装置后达到预设的要求？
答题要求：请你在解答时，画出必要的示意图，并用必要的计算、推理和文字来说明你的理由．（下面给出了几个边长为30km的正方形城区示意图，供解题时选用）

图1               图2                  图3                图4

如图，△ABC中，已知∠BAC＝45°，AD⊥BC于D，BD＝2，DC＝3，求AD的长.
小萍同学灵活运用轴对称知识，将图形进行翻折变换，巧妙地解答了此题.请按照小萍的思路，探究并解答下列问题：
(1) 分别以AB、AC为对称轴，画出△ABD、△ACD的轴对称图形，D点的对称点为E、F，延长EB、FC相交于G点，求证：四边形AEGF是正方形；
(2) 设AD=x，建立关于x的方程模型，求出x的值.

下列命题中，正确的是                                        （     ）

A．四边相等的四边形是正方形	B．四角相等的四边形是正方形
C．对角线相等的菱形是正方形	D．对角线垂直且相等的四边形是正方形

如图，在平面直角坐标系中，,,,,……，以为对角线作第一个正方形，以为对角线作第二个正方形，以为对角线作第三个正方形，……，顶点，，，……都在第一象限，按照这样的规律依次进行下去，点的坐标为_________________．
               

已知：如图(1)，在平行四边形ABCD中，对角线CA⊥BA，AB＝AC＝8cm，四边形A₁B₁C₁D₁是平行四边形ABCD绕点A按逆时针方向旋转45°得到的，A₁D₁经过点C，B₁C₁分别与AB、BC相交于点P、Q．
（1）求四边形CD₁C₁Q的周长；(保留无理数，下同)
（2）求两个平行四边形重合部分的四边形APQC的面积S；
（3）如图(2)，将平行四边形A₁B₁C₁D₁以每秒1cm的速度向右匀速运动，当运动到B₁C₁在直线AC上时停止运动．设运动的时间为x（秒），两个平行四边形重合部分的面积为y（cm²）．求y关于x的函数关系式，并探索是否存在一个时刻x，使得y取最大值，若存在，请你求出这个最大值；若不存在，请你说明理由．

甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好都是9.4环,
方差分别是,,,.在本次射击测试中,成绩最
稳定的是

A．甲

B．乙

C．丙

D．丁

随机从甲、乙两块试验田中各抽取100株麦苗测量高度，计算平均数和方差的结果为：，，，，则小麦长势比较整齐的试验田是   (填“甲”或“乙”)

如图1，点O为直线AB上一点，过点O作射线OC，使∠AOC=60°．将一把直角三角尺的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方，其中∠OMN=30°。

（1）将图1中的三角尺绕点O顺时针旋转至图2，使一边OM在∠BOC的内部，且恰好平分∠BOC，求∠CON的度数；
（2）将图1中的三角尺绕点O按每秒10°的速度沿顺时针方向旋转一周，在旋转的过程中，在第        秒时，边MN恰好与射线OC平行；在第        秒时，直线ON恰好平分锐角∠AOC。（直接写出结果）；
（3）将图1中的三角尺绕点O顺时针旋转至图3，使ON在∠AOC的内部，请探究∠AOM与∠NOC之间的数量关系，并说明理由．

如图，已知抛物线经过O(0,0)，A(4,0),B(3,)三点，连接AB，过点B作BC∥轴交该抛物线于点C.

求这条抛物线的函数关系式.
两个动点P、Q分别从O、A同时出发,以每秒1个单位长度的速度运动. 其中，点P沿着线段0A向A点运动，点Q沿着线段AB向B点运动. 设这两个动点运动的时间为（秒) (0＜≤2)，△PQA的面积记为S.
① 求S与的函数关系式；
② 当为何值时，S有最大值，最大值是多少？并指出此时△PQA的形状；
是否存在这样的值，使得△PQA是直角三角形?若存在，请直接写出此时P、Q两点的坐标；若不存在，请说明理由.

老师问A、B、C、D、E五位学生：“昨天你们有几个人玩过游戏？”他们的回答分别为A：
没有人；B：一个人；C：二个人；D；三个人；E：四个人。老师知道：他们之中有人玩过
游戏，也有人没有玩过游戏。若没有玩过游戏的人说的是真话，那么他们5个人中有     个
人玩过游戏。