从美学角度来说,人的上身长与下身长之比为黄金比时,可以给人一种协调的美感。某女老师上身长约61.80cm,下身长约93.0 0cm,她要穿约________cm的高跟鞋才能达到黄金比的美感效果(精确到0.01cm)
0cm,她要穿约________cm的高跟鞋才能达到黄金比的美感效果(精确到0.01cm)
下列命题中,真命题是( )
| A.对角线互相垂直且相等的四边形是正方形 |
| B.等腰梯形既是轴对称图形又是中心对称图形 |
| C.圆的切线垂直于经过切点的半径 |
| D.垂直于同一直线的两条直线互相垂直 |
在直角坐标系中,正方形 、
、 、…、
、…、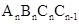 按如图所示的方式放置,其中点
按如图所示的方式放置,其中点 …、
…、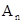 均在一次函数
均在一次函数 的图象上,点
的图象上,点 …、
…、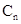 均在x轴上.若点
均在x轴上.若点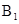 的坐标为(1,1),点
的坐标为(1,1),点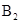 的坐标为(3,2),则点
的坐标为(3,2),则点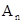 的坐标为_________
的坐标为_________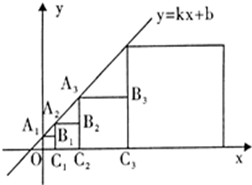
(11·漳州)用形状和大小相同的黑色棋子按下图所示的方式排列,按照这样的规律,第n个图形需要棋子_ ▲ 枚.(用含n的代数式表示)
(11·漳州)下列命题中,假命题是
| A.经过两点有且只有一条直线 | B.平行四边形的对角线相等 |
| C.两腰相等的梯形叫做等腰梯形 | D.圆的切线垂直于经过切点的半径 |
下列命题中,正确的是( )
| A.过一点作已知直线的平行线有一条且只有一条 |
| B.对角线相等的四边形是矩形 |
| C.两条边及一个角对应相等的两个三角形全等 |
| D.位似图形一定是相似图形 |
小英早上从家里骑车上学,途中想到社会实践调查资料忘带了,立刻原路返回,返家途中遇到给她送资料的妈妈,接过资料后,小英加速向学校赶去.能反映她离家距离s与骑车时间t的函数关系图象大致是
(11·珠海)如图,在鱼塘两侧有两棵树A、B,小华要测量此
两树之间的距离.他在距A树30 m的C处测得∠ACB=30°,又在B处测得∠ABC=120°.求
A、B两树之间的距离(结果精确到0.1m)(参考数据:

.在一次课题设计活动中,小明对修建一座87m长的水库大坝提出了以下方案;大坝的横截面为等腰梯形,如图, ∥
∥ ,坝高10m,迎水坡面
,坝高10m,迎水坡面 的坡度
的坡度 ,老师看后,从力学的角度对此方案提出了建议,小明决定在原方案的基础上,将迎水坡面
,老师看后,从力学的角度对此方案提出了建议,小明决定在原方案的基础上,将迎水坡面 的坡度进行修改,修改后的迎水坡面
的坡度进行修改,修改后的迎水坡面 的坡度
的坡度 。
。

(1) 求原方案中此大坝迎水坡 的长(结果保留根号)
的长(结果保留根号)
(2) 如果方案修改前后,修建大坝所需土石方总体积不变,在方案修改后,若坝顶沿 方向拓宽2.7m,求坝顶将会沿
方向拓宽2.7m,求坝顶将会沿 方向加宽多少米?
方向加宽多少米?
把棱长为4的正方体分割成29个棱长为整数的正方体(且没有剩余),其中棱长为1的正方体的个数为 .
某学校要在围墙旁建一个长方形的中药材种植实习苗圃,苗圃的一边靠围墙(墙的长度不限),另三边用木栏围成,建成的苗圃为如图所示的长方形ABCD.已知木栏总长为120米,设AB边的长为x米,长方形ABCD的面积为S平方米.
(1)求S与x之间的函数关系式(不要求写出自变量x的取值范围).当x为何值时,S取得最值(请指出是最大值还是最小值)?并求出这个最值;
(2)学校计划将苗圃内药材种植区域设计为如图所示的两个相外切的等圆,其圆心分别为O1和O2,且O1到AB、BC、AD的距离与O2到CD、BC、AD的距离都相等,并要求在苗圃内药材种植区域外四周至少要留够0.5米宽的平直路面,以方便同学们参观学习.当(l)中S取得最值时,请问这个设计是否可行?若可行,求出圆的半径;若不可行,请说明理由.
如图,在亚丁湾一海域执行护航任务的我海军某军舰由东向西行驶.在航行到B处时,发现灯塔A在我军舰的正北方向500米处;当该军舰从B处向正西方向行驶至达C处时,发现灯塔A在我军舰的北偏东60°的方向.求该军舰行驶的路程.(计算过程和结果均不取近似值)