2011年湖北潜江 仙桃 天门 江汉油田中考数学卷
探究
如图①,在□ABCD的形外分别作等腰直角△ABF和等腰直角△ADE,∠FAB=∠EAD=90°,连结AC、EF.在图中找一个与△FAE全等的三角形,并加以证明.
应用
以□ABCD的四条边为边,在其形外分别作正方形,如图②,连结EF、GH、IJ、KL.若□ABCD的面积为5,则图中阴影部分四个三角形的面积和为 .
甲、乙两组工人同时加工某种零件,乙组工作中有一次停产更换设备,更换设备
后,乙组的工作效率是原来的2倍.两组各自加工零件的数量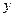 (件)与时间
(件)与时间 (时)的函数图
(时)的函数图
象如图所示.
(1)求甲组加工零件的数量y与时间 之间的函数关系式.
之间的函数关系式.
(2)求乙组加工零件总量 的值.
的值.
(3)甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱?再经过多长时间恰好装满第2箱?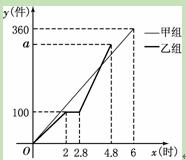
如图,∠C=90°,点A、B在∠C的两边上,CA=30,CB=20,连结AB.点P从
点B出发,以每秒4个单位长度的速度沿BC方向运动,到点C停止.当点P与B、C
两点不重合时,作PD⊥BC交AB于D,作DE⊥AC于E.F为射线CB上一点,且∠CEF=∠ABC.设
点P的运动时间为x(秒).
(1)用含有x的代数式表示CF的长.
(2)求点F与点B重合时x的值.
(3)当点F在线段CB上时,设四边形DECP与四边形DEFB重叠部分图形的面积为y(平方单位).求y与x之间的函数关系式.
(4)当x为某个值时,沿PD将以D、E、F、B为顶点的四边形剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合上述条件的x值.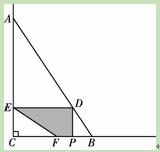
如果60m表示“向北走60m”,那么“向南走40m”可以表示为【 】
| A.-20m | B.-40m | C.20m | D.40m |
甲仓库与乙仓库共存粮450 吨、现从甲仓库运出存粮的60%.从乙仓库运出存粮的40%.结果乙仓库所余的粮食比甲仓库所余的粮食多30 吨。若设甲仓库原来存粮x吨.乙仓库原来存粮y吨,则有
A.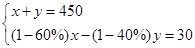 |
B.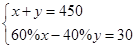 |
C. |
D. |
右面的条形统计图描述了某车间供热那日加工零件数的情况,则这些供热那日加工零件数的平均数、中位数、众数分别是
| A.6.4,10, 4 | B.6, 6,6 | C.6.4,6,6 | D.6,6,10 |

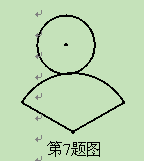
露露从纸上剪下一个圆形和一个扇形纸片(如图),用它们恰好能围成一个圆锥模型。若圆的半径为1,扇形的圆心角等于 ,则此扇形的半径为
如图,梯形ABCD中,AD∥BC,AB=CD,AC⊥BD于点O,∠BAC=60°,若BC=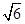 ,则此梯形的面积为
,则此梯形的面积为
| A.2 | B.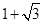 |
C. |
D. |

如图,等边三角形ABC的边长为3,点P为BC边上一点,且BP=1,点D为AC边上一点,若∠APD=60°,则CD的长为
A. |
B. |
C. |
D.1 |
某居民小区为了了解本小区100户居民家庭的平均月使用塑料袋的数量情况,随机调查了10户居民家庭月使用塑料袋的数量,结果如下(单位:只)
65 70 85 74 86 78 74 92 82 94
根据此统计情况,估计该小区这100户居民家庭平均月使用塑料袋为________只。
按如下程序进行运算:
并规定,程序运行到“结果是否大于65”为一次运算,且运算进行4次才停止。则可输入的整数x的个数是_________
如入,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D。
求证:△BEC≌△CDA
第六次人口普查的标准时间是2010年11月1日零时.普查登记的大陆31个省、自治区、直辖市和现役军人的人口共1 339 724 852人.这个数用科学记数法表示为(保留三个有效数字)
A.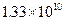 |
B.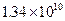 |
C.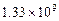 |
D. |
如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点.作△ABC的外接圆⊙ ,则
,则 的长等于
的长等于
A. B.
B.
C.  D.
D.

小英早上从家里骑车上学,途中想到社会实践调查资料忘带了,立刻原路返回,返家途中遇到给她送资料的妈妈,接过资料后,小英加速向学校赶去.能反映她离家距离s与骑车时间t的函数关系图象大致是
如图,已知直线l:y= x,过点A(0,1)作y轴的垂线交直线l于点B,过
x,过点A(0,1)作y轴的垂线交直线l于点B,过
点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点A4的坐标为
| A.(0,64) | B.(0,128) | C.(0,256) | D.(0,512) |

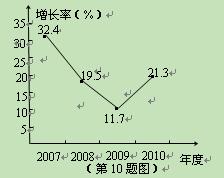
如图是近年来我国年财政收入同比(与上一年比较)增长率的折线统计图,其中2008年我国财政收入约为61330亿元.下列命题:
①2007年我国财政收入约为61330(1-19.5%)亿元;
②这四年中,2009年我国财政收入最少;
③2010年我国财政收入约为61330(1+11.7%)(1+21.3%)亿元.其中正确的有
| A.3个 | B.2个 | C.1个 | D.0个 |
西周戎生青铜编钟是由八个大小不同的小编钟组成,其中最大编钟高度比最小编钟高度的3倍少5cm,且它们的高度相差37 cm.则最大编钟的高度是 cm.
张凯家购置了一辆新车,爸爸妈妈商议确定车牌号,前三位选定为8ZK后,对后两位数字意见有分歧,最后决定由毫不知情的张凯从如图排列的四个数字中随机划去两个,剩下的两个数字从左到右组成两位数,续在8ZK之后,则选中的车牌号为8ZK86的概率是 .
已知□ABCD的周长为28,自顶点A作AE⊥DC于点E,AF⊥BC于点F.若AE=3,AF=4,则CE-CF= .
(满分7分)五月石榴红,枝头鸟儿歌.一只小鸟从石榴树上的A处沿直线飞到对面一房屋的顶部C处.从A处看房屋顶部C处的仰角为 ,看房屋底部D处的俯角为
,看房屋底部D处的俯角为 ,石榴树与该房屋之间的水平距离为
,石榴树与该房屋之间的水平距离为 米,求出小鸟飞行的距离AC和房屋的高度CD.
米,求出小鸟飞行的距离AC和房屋的高度CD.
(满分8分)为迎接市教育局开展的“创先争优”主题演讲活动,某校组织党员教师进行演讲预赛.学校将所有参赛教师的成绩(得分为整数,满分为100分)分成四组,绘制了不完整的统计图表如下:
观察图表信息,回答下列问题:
(1)参赛教师共有 人;
(2)如果将各组的组中值视为该组的平均成绩,请你估算所有参赛教师的平均成绩;
(3)成绩落在第一组的恰好是两男两女四位教师,学校从中随机挑选两位教师参加市教育局组织的决赛.通过列表或画树状图求出挑选的两位教师是一男一女的概率.
(满分8分)如图,BD是⊙O的直径, A、C是⊙O上的两点,且AB=AC,
AD与BC的延长线交于点E.
(1)求证:△ABD∽△AEB;
(2)若AD=1,DE=3,求BD的长.
(满分8分)如图,已知直线AB与 轴交于点C,与双曲线
轴交于点C,与双曲线 交于A(3,
交于A(3, )、B(-5,
)、B(-5, )两点.AD⊥
)两点.AD⊥ 轴于点D,BE∥
轴于点D,BE∥ 轴且与
轴且与 轴交于点E.
轴交于点E.
(1)求点B的坐标及直线AB的解析式;
(2)判断四边形CBED的形状,并说明理由.
(满分10分)2011年4月 25日,全国人大常委会公布《中华人民共和国个人所得税法修正案(草案)》,向社会公开征集意见.草案规定,公民全月工薪不超过3000元的部分不必纳税,超过3000元的部分为全月应纳税所得额.此项税款按下表分段累进计算.
| 级数 |
全月应纳税所得额 |
税率 |
| 1 |
不超过1500元的部分 |
5% |
| 2 |
超过1500元至4500元的部分 |
10% |
| 3 |
超过4500元至9000元的部分 |
20% |
| …… |
…… |
…… |
依据草案规定,解答下列问题:
(1)李工程师的月工薪为8000元,则他每月应当纳税多少元?
(2)若某纳税人的月工薪不超过10000元,他每月的纳税金额能超过月工薪的8%吗? 若能,请给出该纳税人的月工薪范围;若不能,请说明理由.
(满分10分)两个大小相同且含 角的三角板ABC和DEC如图①摆放,使直角顶点重合. 将图①中△DEC绕点C逆时针旋转
角的三角板ABC和DEC如图①摆放,使直角顶点重合. 将图①中△DEC绕点C逆时针旋转 得到图②,点F、G分别是CD、DE与AB的交点,点H是DE与AC的交点.
得到图②,点F、G分别是CD、DE与AB的交点,点H是DE与AC的交点.
(1)不添加辅助线,写出图②中所有与△BCF全等的三角形;
(2)将图②中的△DEC绕点C逆时针旋转 得△D1E1C,点F、G、H的对应点分别为F1、G1、H1,如图③.探究线段D1F1与AH1之间的数量关系,并写出推理过程;
得△D1E1C,点F、G、H的对应点分别为F1、G1、H1,如图③.探究线段D1F1与AH1之间的数量关系,并写出推理过程;
 (3)在(2)的条件下,若D1E1与CE交于点I,求证:G1I =CI.
(3)在(2)的条件下,若D1E1与CE交于点I,求证:G1I =CI.

 =【 】
=【 】








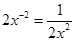
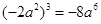
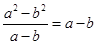
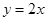 向右平移l个单位后所得图象对应的函数解析式为
向右平移l个单位后所得图象对应的函数解析式为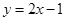

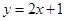
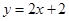
 的一个根为0,则实数a的值为
的一个根为0,则实数a的值为
 在实数范围内有意义,则x的取值范围是_______。
在实数范围内有意义,则x的取值范围是_______。
 的图象与反比例函数
的图象与反比例函数 的图象有一个交点的坐标是(
的图象有一个交点的坐标是( ),则另一个交点的坐标为________。
),则另一个交点的坐标为________。 ,其中
,其中 。
。
 的倒数是
的倒数是




 ,∠CEF=
,∠CEF= ,则∠BCE等于
,则∠BCE等于 




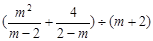 的结果是
的结果是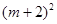
 .
. 轴向上平移5个单位,再沿
轴向上平移5个单位,再沿 轴向左平移4个单位得到点A′,则点A′的坐标是 .
轴向左平移4个单位得到点A′,则点A′的坐标是 . .
. 的两个实数根为
的两个实数根为 、
、 ,且满足
,且满足 ,试求出方程的两个实数根及k的值.
,试求出方程的两个实数根及k的值. 与
与 轴的两个交点
轴的两个交点 = ,b= ,顶点C的坐标为 ;
= ,b= ,顶点C的坐标为 ; 轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号