2011年初中毕业升学考试(广东珠海卷)数学
若⊙O1、⊙O2的半径分别为4和6,圆心距O1O2=8,则⊙O1与⊙O2的位置关系是
| A.内切 | B.相交 | C.外切 | D.外离 |

| A.图象经过点(1,-1) | B.图象位于第二、四象限 |
| C.图象是中心对称图形 | D.当x<0时,y随x的增大而增大 |
某市6月上旬前5天的最高气温如下(单位:℃):28,29,31,29,32.对这组
数据,下列说法正确的是
| A.平均数为30 | B.众数为29 | C.中位数为31 | D.极差为5 |
小亮从家步行到公交车站台,等公交车去学校. 图中的折线表示小亮的行程s(km)与所花时间t(min)之间的函数关系. 下列说法错误的是
| A.他离家8km共用了30min | B.他等公交车时间为6min |
| C.他步行的速度是100m/min | D.公交车的速度是350m/min |

如图,△ABC的顶点都在正方形网格格点上,点A的坐标为(-1,4). 将△ABC
沿y轴翻折到第一象限,则点C的对应点C′的坐标是 ▲ .
将两个形状相同的三角板放置在一张矩形纸片上,按图示画线得到四边形
ABCD,则四边形ABCD的形状是 ▲ .
如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A
为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为 ▲ cm.
将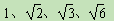 按右侧方式排列.若规定(m,n)表示第m排从左向右
按右侧方式排列.若规定(m,n)表示第m排从左向右
第n个数,则(5,4)与(15,7)表示的两数之积是 ▲ .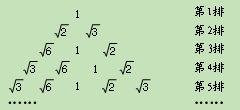
小明有3支水笔,分别为红色、蓝色、黑色;有2块橡皮,
分别为白色、灰色.小明从中任意取出1支水笔和1块橡皮配套使用.试用树状图或表格列
出所有可能的结果,并求取出红色水笔和白色橡皮配套的概率.
为迎接建党90周年,某校组织了以“党在我心中”为主题
的电子小报制作比赛,评分结果只有60,70,80,90,100五种.现从中随机抽取部分作
品,对其份数及成绩进行整理,制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)求本次抽取了多少份作品,并补全两幅统计图;
(2)已知该校收到参赛作品共900份,请估计该校学生比赛成绩达到90分以上(含90分)的作品有多少份?
已知二次函数
(1)在给定的直角坐标系中,画出这个函数的图象;
(2)根据图象,写出当
时,
的取值范围;
(3)若将此图象沿
轴向右平移3个单位,请写出平移后图象所对应的函数关系式.

如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯
罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD="60°." 使用发现,光线最
佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?

如图,在△ABC中,∠C= 90°,以AB上一点O为圆心,
OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.
(1)若AC=6,AB= 10,求⊙O的半径;
(2)连接OE、ED、DF、EF.若四边形BDEF是平行四边形,试判断四边形OFDE的形状,并说明理由.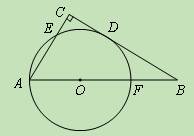
(11·珠海)已知一组数据:4,-1,5,9,7,6,7,则这组数据的极差是
| A.10 | B.9 | C.8 | D.7 |
(11·珠海)某校为了调查学生视力变化情况,从该校2008年
入校的学生中抽取了部分学生进行连续三年的视力跟踪调查,将所得数据处理,制成拆线统
计图和扇形统计图,如图所示: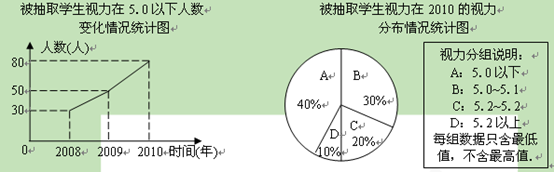
(1)该校被抽查的学生共有多少名?
(2)现规定视力5.1及以上为合格,若被抽查年级共有600名学生,估计该年级在2010年有多少名学生视力合格.
(11·珠海)如图,在Rt△ABC中,∠C=90°.
(1)求作:△ABC的一条中位线,与AB交于D点,与BC交于E点.(保留作图痕迹,不
写作法)
(2)若AC=6,AB=10,连结CD,则DE=_ ▲ ,CD=_ ▲ .
(11·珠海)八年级学生到距离学校15千米的农科所参观,一部分学生骑自行车先走,过了40分钟后,其余同学乘汽车出发,结果两者同时到达.若汽车的速度是骑自行车同学速度的3倍,求骑自行车同学的速度.
(11· 珠海)如图,在正方形ABC1D1中,AB=1.连接AC1,
珠海)如图,在正方形ABC1D1中,AB=1.连接AC1,
以AC1为边作第二个正方形AC1C2D2;连接AC2,以AC2为边作第三个正方形AC2C3D3.
(1)求第二个正方形AC1C2D2和第三个正方形的边长AC2C3D3;
(2)请直接写出按此规律所作的第7个正方形的边长.
(11·珠海)如图,在鱼塘两侧有两棵树A、B,小华要测量此
两树之间的距离.他在距A树30 m的C处测得∠ACB=30°,又在B处测得∠ABC=120°.求
A、B两树之间的距离(结果精确到0.1m)(参考数据:

(11·珠海)(本题 满分7分)某校为庆祝国庆节举办游园活动,小军来到摸球
满分7分)某校为庆祝国庆节举办游园活动,小军来到摸球
兑奖活动场地,李老师对小军说:“这里有A、B两个盒子,里面都装有一些乒乓球,你只
能选择在其中一只盒子中摸球.”获将规则如下:在A盒中有白色乒乓球4个,红色乒乓球
2个,一人只能摸一次且一次摸出一个球,若为红球则可获得玩具熊一个,否则不得奖;在
B盒中有白色乒乓球2个,红色乒乓球2个,一人只能摸一次且一次摸出两个球,若两球均
为红球则可获得玩具熊一个,否则不得奖.请问小军在哪只盒子内摸球获得玩具熊的机会更
大?说明你的理由.
(11·珠海)如图,Rt△OAB中,∠OAB=90°,O为坐标原点,
边OA在x轴上,OA=AB=1个单位长度.把Rt△OAB沿x轴正方向平移1个单位长度后
得△AA1B.
(1)求以A为顶点,且经过点B1的抛物线的解析式;
(2)若(1)中的抛物线与OB交于点C,与y轴交于点D,求点D、C的坐标.
(11·珠海)如图,将一个钝角△ABC(其中∠ABC=120°)绕
点B顺时针旋转得△A1BC1,使得C点落在AB的延长线上的点C1处,连结AA1.
(1)写出旋转角的度数;
(2)求证:∠A1AC=∠C1.
(11·珠海)已知:如图,锐角△ABC内接于⊙O,∠ABC=45°;
点D是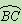 上一点,过点D的切线DE交AC的延长线于点E,且DE∥BC;连结AD、BD、
上一点,过点D的切线DE交AC的延长线于点E,且DE∥BC;连结AD、BD、
BE,AD的垂线AF与DC的延长线交于点F.
(1)求证:△ABD∽△ADE;
(2)记△DAF、△BAE的面积分别为S△DAF、S△BAE,求证:S△DAF>S△BAE.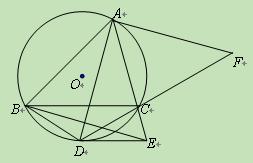







 D.不变
D.不变




 P(P与D点不重
P(P与D点不重

 粤公网安备 44130202000953号
粤公网安备 44130202000953号