（11·
珠海）如图，在正方形ABC1D1中，AB＝1．连接AC1，
以AC1为边作第二个正方形AC1C2D2；连接AC2，以AC2为边作第三个正方形AC2C3D3．
（1）求第二个正方形AC1C2D2和第三个正方形的边长AC2C3D3；
（2）请直接写出按此规律所作的第7个正方形的边长．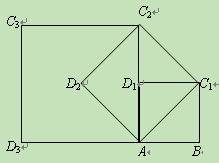
的5倍比它的2倍大3；
与4的差等于它的相反数；
，求
的值。
，0，
，
，
，其中
。
相关知识点
推荐套卷
（11·珠海）如图，在正方形ABC1D1中，AB＝1．连接AC1，
以AC1为边作第二个正方形AC1C2D2；连接AC2，以AC2为边作第三个正方形AC2C3D3．
（1）求第二个正方形AC1C2D2和第三个正方形的边长AC2C3D3；
（2）请直接写出按此规律所作的第7个正方形的边长．
粤公网安备 44130202000953号