安徽省泗县初二上学期期末数学卷
两年前某种药品每吨的生产成本是5000元,随着生产技术的进步,现在生产这种药品的成本是每吨3000元,假设这两年成本的平均下降北一样,那么该药品成本的年平均下降率是多少?(精确到0.1%)
如图,平面直角坐标系中,矩形 的顶点
的顶点 在原点,点
在原点,点 在
在 轴的正半轴上,点
轴的正半轴上,点 在
在 轴的正半轴上.已知
轴的正半轴上.已知 ,
, ,
, 是
是 的中点,
的中点, 是
是 的中点.
的中点.
(1)分别写出点 、点
、点 的坐标;
的坐标;
(2)过点 作
作 交
交 轴于点
轴于点 ,求点
,求点 的坐标;
的坐标;
(3)在线段 上是否存在点
上是否存在点 ,使得以点
,使得以点 、
、 、
、 为顶点的三角形是等腰三角形,若存在,求出点
为顶点的三角形是等腰三角形,若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
去年我国发现的首例甲型H1N1流感确诊病例曾在成都某医院隔离观察,要掌握他在一周内的体温是否稳定,则医生需要了解这位病人7天体温的 ( )
| A.中位数 | B.平均数 | C.方差 | D.众数 |
用配方法解方程 x 2 -2x-5=0时,原方程应变形为 ( )
| A.(x-1)2 ="6" | B.(x + 1)2 ="6" | C.(x + 1)2 ="9" | D.(x-2)2 =9 |
下列说法中错误的是 ( )
| A.一组对边平行且一组对角相等的四边形是平行四边形 | |
| B.对角线互相垂直的平行四边形是正方形 | |
| C.四个角相等的四边形是矩形 | D.每组邻边都相等的四边形是菱形 |
如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于 ( )
| A.12cm | B.10cm | C.8cm | D.6cm |
如图,梯形ABCD中,∠ABC和∠DCB的平分线相交于梯形中位线EF上的一点P,若EF=3,则梯形ABCD的周长为 ( )
| A.9 | B.10.5 | C.12 | D.15 |
如图,折叠直角梯形纸片的上底AD,点D落在底边BC上点F处,已知DC=8㎝,FC = 4㎝,则EC长 ㎝.
已知一元二次方程a 2+b
2+b +c=0(a≠0)的两根分别为
+c=0(a≠0)的两根分别为 1、
1、 2,则有
2,则有 1+
1+ 2=
2= ;
; 1
1 2=
2= .
.
请应用以上结论解答下列问题:
已知方程x2-4x -1=0有两个实数根x1,x2, 要求不解方程,
求值:(1)(x1+1)(x2+1) (2)
如图,在平行四边形ABCD中,∠ABC、∠BCD的平分线相交于点O,BO延长线交CD延长线于点E,
求证:OB=OE
如图,DB∥AC,且DB=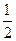 AC,E是AC的中点,
AC,E是AC的中点,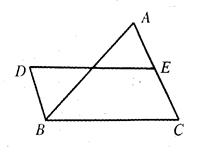
(1 )求证:BC=DE;
)求证:BC=DE;
(2)连结AD、BE,若要使四边形DBEA是矩形,则给△ABC添加一个什么条件,为什么?
(3)在(2)的条件下,若要使四边形DBEA是正方形,则∠C=" " 0
下列四组数据,能作为直角三角形的三边长的是
| A. 1,2,3 | B. 2,3,4 | C.3, 4,5 | D.4,5, 6 |
如图2,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕点B按顺时针转动一个角度到A1BC1的位置,使得点A、B、C1在同一条直线上,那么这个旋转角度数是
A.120° B.90° C. 60° D. 30°
在平面直角坐标系中,位于第四象限的点是
| A.(-1,-3) | B.(2,1) | C.(-2,1) | D.(1,-2) |
小华的妈妈是一位皮鞋经销部的经理,为了解鞋子的销售情况,她最感兴趣的数据代表是( )
A.中位数 B.众数 C. 加权平均数 D 平均数
小明拿一张50元的人民币到银行等额换取5元或10元的人民币,请问小明换钱方式有( )种.
| A.4 | B.5 | C.6 | D.7 |
如图,点P是矩形ABCD的边AD的一个动点,矩形的两条边AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是( )
A.2.5 B.1.2 C.2.4 D.4.8
10年前,小明的爸爸的年龄是小明的6倍;10年后,小明爸爸的年龄是小明的2倍,则小明现在的年龄是__________
某校欲招聘一名数学教师,学校对甲、乙、丙三位候选人进行了三项能力测试,各项测试成绩满分均为100分,根据结果择优录用.三位候选人的各项测试成绩如下表所示:
| 测试项目 |
测试成绩 |
||
| 甲 |
乙 |
丙 |
|
| 教学能力 |
85 |
73 |
73 |
| 科研能力 |
70 |
71 |
65 |
| 组织能力 |
64 |
72 |
84 |
(1)如果根据三项测试的平均成绩,谁将被录用,说明理由;
(2)根据实际需要,学校将教学、科研和组织三项能力测试得分按5∶3∶2的比例确定每人的成绩,谁将被录用,说明理由
在直角坐标系中,描出点(0,3),(2,2),(3,0),(4,2),(6,3).(4,4),(3,6),(2,4),(0,3),并将各点用线段依次连接起来.
(1)观察这组点组成的图形,你觉得它像________________________.
(2)研究这个图形的轴对称性和中心对称性.____________________________.
(3)上面各点的横坐标不变,纵坐标分别缩小为原来的一半.按同样的方法将所得各点连接起来,(4)与原图形相比,所得图形有什么变化?_________________.
(4)将横坐标分别变为原来的相反数,纵坐标不变,按同样的方法将所得各点连接起来,与原图形相比,所得图形有什么变化? ________________.
(5)将横、纵坐标分别变为原来的相反数,按同样的方法将所得各点连接起来,与原图形相比,所得图形有什么变化?______________________________________________.
(6)纵坐标不变,横坐标分别缩小为原来的一半,按同样的方法将所得各点连接起来,与原图形相比,所得图形有什么变化?______________________________.
(7)将横坐标分别减2,纵坐标分别减1,按同样的方法将所得各点连接起来,与原图形相比,所得图形有什么变化?_________________________
泗县某校八年级1班20名学生某次数学测试的成绩统计如表:
| 成绩 |
60 |
70 |
80 |
90 |
100 |
| 人数(人) |
1 |
5 |
x |
y |
2 |
(1)如果这20名学生数学测试成绩的平均分是82分,求x、y的值;
(2)在(1)的条件下,设20名学生本次数学测试成绩的众数是m,中位数为n,求 的值
的值
如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.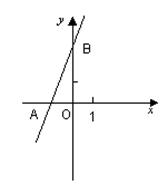
(1)求A,B两点的坐标;
(2)过B点作直线BP与x轴相交于P,且使OP=2OA, 求ΔABP的面积.
在平面内,旋转变换是指某一图形绕一个定点按顺时针或逆时针旋转一定的角度得到新位置图形的一种变换.
活动一:如图l,在Rt△ABC中,D为斜边AB上的一点,AD =2,BD =1,且四边形DECF是正方形,在求阴影部分面积时,小明运用图形旋转的方法,将△DBF绕点D逆时针旋转90°,得到△DGE(如图2所示),小明一眼就看出答案,请你写出阴影部分的面积:________.
活动二:如图3,在四边形ABCD中,AB=AD,∠BAD=∠C=90°,BC =5,CD =3,过点A作AE⊥BC,垂足为点E,小明仍运用图形旋转的方法,将△ABE绕点A逆时针旋转90°,得到△ADC(如图4所示),则:
(1)四边形AECG是怎样的特殊四边形?答:___________;
(2)AE的长是______________.
活动三:如图5,在四边形ABCD中,AB⊥AD,CD⊥AD,将BC绕点B逆时针 旋转90°得到线段BE,连结AE.若AB =2,DC =4,求△ABE的面积.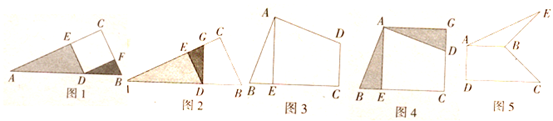
 中,
中, ,
, 是
是 上一点,且
上一点,且 .
.
 ;
; ,
, ,求
,求 ,求
,求 的度数.
的度数. ( )
( )



 ,则
,则 的取值范围是 ( )
的取值范围是 ( )







 ;
;  ="_____" __
="_____" __ 有意义
有意义 的解为
的解为 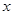 ,5,它的平均数是3,则这个样本的极差是___
,5,它的平均数是3,则这个样本的极差是___ 的值在连续整数 和 之间.
的值在连续整数 和 之间.












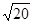 (误差小于0.1)≈_________
(误差小于0.1)≈_________
 (2)
(2)
 粤公网安备 44130202000953号
粤公网安备 44130202000953号