为了测量学校一棵参天古树的高度,我校数学兴趣小组做了如下探索:
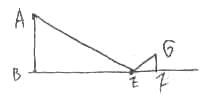
实践1:利用一根标竿和一根皮尺设计出如图1的测量方案,把长为2.5米的标竿竖直插入离树(AB)8.7米的点E处,然后沿着直线BE后退到点D,这时眼睛恰好通过标竿顶点F,看到树的顶点A。再用皮尺测得DE=2.7米。观察者目高CD=1.6米。他们利用相似原理求得树高为5.4米。
实践2:提供选用的测量工具有①皮尺一根、②教学用三角板一副、③镜子一面、④测角仪一个。请你设计测量方案,并根据你所设计的测量方案回答下列问题。
(1)在你设计的方案中,选用的测量工具是(用工具的序号填写)。
(2)在图2中画出你测量方案的示意图。
(3)你需要测得示意图中哪些数据。并分别用a、b、c等表示测得数据。
(4)写出求树高(AB)的等式,AB=。(用a、b、c等字母表示)