福建省惠安县初三上学期末数学卷
某校为了研究中学生是否应带手机到校园,现委托学生会对同学带手机到校园的主要用途进行调查统计,经统计整理,绘制成不完整的扇形统计图与条形统计图如下,请回答如下问题:
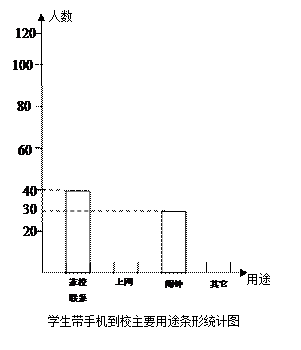
(1)本次共调查了多少人?
(2)请计算出学生带手机主要用于上网的人数;
(3)分别把条形统计图和扇形统计图补充完整(标出角度及百分比)
出租车收费标准因地而异. A市为:行程不超过3千米收起步价12元,超过3千米后每千米增收1.2元;B市为:行程不超过3千米收起步价10元,超过3千米后每千米增收1.4元.设在A、B两市乘坐出租车
 千米.
千米.
(1)若小明分别在A、B两市乘坐出租车行驶了相同的行程8千米,试分别计算出两次乘车的费用;
(2)在A、B两市乘坐出租车 千米
千米 的费用相差多少元,试用含
的费用相差多少元,试用含 的代数式表示
的代数式表示
下列各组中的四条线段成比例的是( ).
| A.4cm、2cm、1cm、3cm | B.1cm、2cm、3cm、5cm |
| C.3cm、4cm、5cm、6cm | D.1cm、2cm、2cm、4cm |
一个袋子中装有4只白球和若干只红球,这些球除颜色外其余均相同,搅匀后,从袋子中随机摸出一个球是红球的概率是 ,则袋中有红球( ).
,则袋中有红球( ).
| A.3只 | B.6只 | C.8只 | D.12只 |
根据下列表格中的对应值:
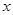 |
0.75 |
0.8 |
0.85 |
0.9 |
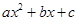 |
-0.25 |
-0.04 |
0.19 |
0.44 |
判断方程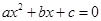 (
(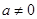 ,
,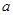 、
、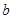 、
、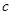 为常数)一个解
为常数)一个解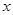 的范围最可能是( ).
的范围最可能是( ).
A.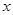 <0.75 B.0.75<
<0.75 B.0.75<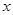 <0.8 C.0.8<
<0.8 C.0.8<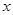 <0.85 D.0.85<
<0.85 D.0.85<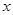 <0.9
<0.9
如图,△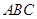 的三个顶点坐标分别是
的三个顶点坐标分别是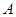 (0,1),
(0,1),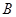 (2,3),
(2,3),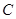 (3,0),
(3,0),
经过平移后得到△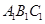 ,其中
,其中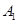 的坐标为(3,1),则
的坐标为(3,1),则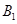 的坐标为
的坐标为 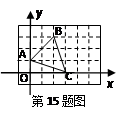
如图△ 中,
中, ,
, ,
, =12cm,把△
=12cm,把△ 绕着它的斜边中点
绕着它的斜边中点 逆时针旋转
逆时针旋转 至△
至△ 的位置,
的位置, 交
交 于点
于点 .
.
(1) = cm.
= cm.
(2)△ 与△
与△ 重叠部分的面积为 cm2
重叠部分的面积为 cm2
解方程 时,有一位同学解答如下:
时,有一位同学解答如下:
∵ ,
, 
∴
∴ ,
,
请你分析以上解答有无错误,如有错误,请指出错误的地方,并写出正确的解题过程.
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ 的顶点都在格点上,在方格纸中建立平面直角坐标系如图所示.
的顶点都在格点上,在方格纸中建立平面直角坐标系如图所示.
(1)画出△ 关于
关于 轴的对称图形△
轴的对称图形△ ,并写出△
,并写出△ 各顶点的坐标.
各顶点的坐标.
(2)把(1)中的△ 绕着点
绕着点 顺时针旋转
顺时针旋转 得到△
得到△ ,在图中画出△
,在图中画出△ ,并回答△
,并回答△ 与△
与△ 对应顶点的坐标有何关系
对应顶点的坐标有何关系
如图,小明站在离树20m的 处测得树顶的仰角为
处测得树顶的仰角为 ,已知小明的眼睛(点
,已知小明的眼睛(点 )离地面约1.6m,求树的高度.(精确到0.1m)
)离地面约1.6m,求树的高度.(精确到0.1m)
在一个箱子中放有三张完全相同的卡片,卡片上分别标有数字1,2,3.从箱子中任意取出一张卡片,用卡片上的数字作为十位数字,然后放回,再取出一张卡片,用卡片上的数字作为个位数字,这样组成一个两位数,请用列表法或画树状图的方法完成下列问题.
(1)按这种方法能组成哪些两位数?
(2)组成的两位数是3的倍数的概率是多少?
下列说法正确的是( )
| A.“明天降雨的概率是80%”表示明天有80%的时间降雨 |
| B.“抛一枚硬币正面朝上的概率是0.5”表示每抛硬币10次有5次出现正面朝上 |
| C.“彩票中奖的概率是1%”表示买100张彩票一定会中奖 |
| D.抛掷一枚图钉,针尖触地和针尖朝上的概率不相等 |
如图,小明在打网球时,要使球恰好能打过网,而且落在离网5米的位置上,则球拍拍球的高度 应为( )
应为( )
| A.2.7米 | B.1.8米 | C.0.9米 | D.6米 |
在△ABC中,AB=12,AC=10,BC=9,AD是BC边上的高.将△ABC按如图所示的方式折叠,使点A与点D重合,折痕为EF,则△DEF的周长为( )
| A.9.5 | B.10.5 | C.11 | D.15.5 |
如图是一个质量均匀的圆形转盘,圆盘被等分成黑、红、白三部分,轻轻转动圆盘,则指针恰好指在红色部分的概率是__________
据某市交通部门统计,该市2008年底全市汽车拥有量为150万辆,而截止到2010年底,全市的汽车拥有量已达216万辆.设这两年中汽车平均每年增长的百分率为 ,则可列方程为:
,则可列方程为:
如图所示,已知:点 ,
, ,
,  .在
.在 内依次作等边三角形,使其一边在
内依次作等边三角形,使其一边在 轴上,另一个顶点在
轴上,另一个顶点在 边上,作出的等边三角形分别是第1个
边上,作出的等边三角形分别是第1个 ,第2个
,第2个 ,第3个
,第3个 ,…,则①
,…,则① = 度;②
= 度;② =
=
如图, 与
与 是位似图形,且顶点都在格点上.
是位似图形,且顶点都在格点上.
(1) 在图上标出位似中心D的位置,并写出该位似中心D的坐标是 ;
(2)△ABC与△A/B/C/的相似比为
某高铁工程即将动工,工程需要测量某一条河的宽度.如图,一测量员在河岸边的A处测得对岸岸边的一根标杆B在它的正北方向,测量员从A点开始沿岸边向正东方向前进100米到达点C处,测得标杆B在北偏西280处.求河宽AB.(结果精确到1米)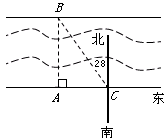
如图,AC平分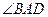 ,
,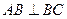 ,垂足为点B,
,垂足为点B,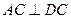 ,垂足为点C.
,垂足为点C.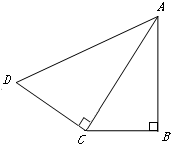
(1)请你判断△ABC与△ACD是否相似,并说明理由;
(2)若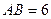 ,
,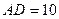 ,求AC的长.
,求AC的长.
在一块长16m,宽12m的矩形荒地上,要建造一个花园,要求花园面积是荒地面积的一半,且整体图案成轴对称图形.下面是小华、小芳与小明的设计方案.
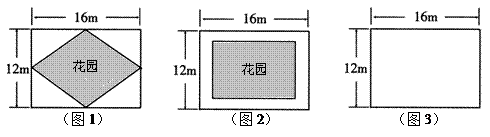
请你根据以上的对话,完成下列问题.
(1)你认为小华所设计的花园的形状是 ,整个设计图案共有 条对称轴;
(2)请你帮助小芳计算出道路的宽度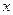 的值;
的值;
(3)请你根据小明的设计方案在图3中画出符合设计条件的草图,然后根据你所画的草图求出该等腰梯形的上底和下底的长.
如图1,已知直线 的解析式为
的解析式为 ,它与
,它与 轴、y轴分别相交于A、B两点.点C从点O出发沿OA以每秒1个单位的速度向点A匀速运动;点D从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,点C、D同时出发,当点C到达点A时同时停止运动.伴随着C、D的运动,EF始终保持垂直平分CD,垂足为E,且EF交折线AB-BO-AO于点F.
轴、y轴分别相交于A、B两点.点C从点O出发沿OA以每秒1个单位的速度向点A匀速运动;点D从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,点C、D同时出发,当点C到达点A时同时停止运动.伴随着C、D的运动,EF始终保持垂直平分CD,垂足为E,且EF交折线AB-BO-AO于点F.
(1)直接写出A、B两点的坐标;
(2) 设点C、D的运动时间是t秒(t>0).
①用含t的代数式分别表示线段AD和AC的长度;
②在点F运动的过程中,四边形BDEF能否成为直角梯形?若能求t的值;若不能,请说明理由.(可利用备用图解题)




 的根是( ).
的根是( ). ,
,
 ,
,
 ,
,
 (3,0),点
(3,0),点 (0,-4),则
(0,-4),则 的值为( ).
的值为( ).




 的边长为6cm,点
的边长为6cm,点 是重心,则点
是重心,则点
 cm
cm cm
cm cm
cm cm
cm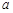 时,二次根式
时,二次根式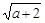 有意义
有意义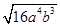 =
=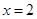 是关于
是关于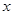 的一元二次方程
的一元二次方程 的一根,那么
的一根,那么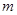 =
=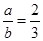 ,则
,则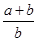 =
=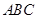 中,
中,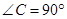 ,如果
,如果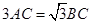 ,则
,则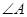 的度数是
的度数是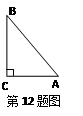
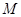 、
、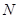 、
、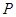 分别是△
分别是△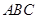 三边的中点,若△
三边的中点,若△ 的周长为 cm
的周长为 cm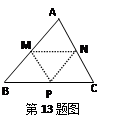
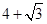 的积不含二次根式
的积不含二次根式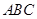 的两直角边的长都是方程
的两直角边的长都是方程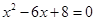 的根,则Rt△
的根,则Rt△
 ,其中
,其中
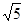
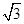

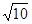
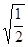
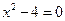 的解是( )
的解是( )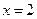
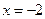
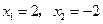
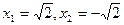
 ,下列配方正确的是( )
,下列配方正确的是( )



 中,∠C=90°,BC=3cm,AC=4cm,则
中,∠C=90°,BC=3cm,AC=4cm,则 的值为( ).
的值为( ).



 ____________时,二次根式
____________时,二次根式 在实数范围内有意义
在实数范围内有意义 =" "
=" " ,则
,则 ____________
____________ ,则该坡的坡角
,则该坡的坡角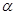 =
= 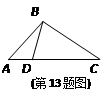
 是方程
是方程 的一个实数根,则
的一个实数根,则 的值是
的值是  在边
在边 上,
上, ,连接
,连接 交
交 于点
于点 ,则
,则 的面积与
的面积与 的面积之比为_______
的面积之比为_______
 ②
②
 . ②
. ②
 ,其中a=3,b=
,其中a=3,b=
 粤公网安备 44130202000953号
粤公网安备 44130202000953号