如图1,水坝的横截面是梯形 , ,坝顶 ,背水坡 的坡度 (即 为 ,坝底 .

(1)求坝高;
(2)如图2,为了提高堤坝的防洪抗洪能力,防汛指挥部决定在背水坡将坝顶和坝底同时拓宽加固,使得 , ,求 的长.(参考数据: , ,
汛期即将来临,为保证市民的生命和财产安全,市政府决定对一段长200米且横断面为梯形的大坝用土石进行加固.如图,加固前大坝背水坡坡面从至
共有30级阶梯,平均每级阶梯高
,斜坡
的坡度
;加固后,坝顶宽度增加2米,斜坡
的坡度
,问工程完工后,共需土石多少立方米?(计算土石方时忽略阶梯,结果保留根号)

如图,这是一座一侧有缓步台的过街天桥示意图.已知桥面 长为 ,与水平面的垂直距离为 ,桥面 长为 ,与水平面的垂直距离为 .斜坡 , 与水平面的夹角分别为 , ,斜坡 的坡度(即 为 .求天桥跨度 的长.
参考数据: , ,

如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部 点处测得旗杆顶端的仰角 ,升旗台底部到教学楼底部的距离 米,升旗台坡面 的坡度 ,坡长 米,若旗杆底部到坡面 的水平距离 米,则旗杆 的高度约为 (参考数据: , ,

| A. |
12.6米 |
B. |
13.1米 |
C. |
14.7米 |
D. |
16.3米 |
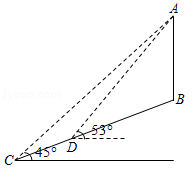
如图,垂直于水平面的 信号塔 AB建在垂直于水平面的悬崖边 B点处,某测量员从山脚 C点出发沿水平方向前行78米到 D点(点 A, B, C在同一直线上),再沿斜坡 方向前行78米到 E点(点 A, B, C, D, E在同一平面内),在点 E处测得 信号塔顶端 A的仰角为43°,悬崖 BC的高为144.5米,斜坡 DE的坡度(或坡比) ,则信号塔 AB的高度约为( )
(参考数据: , , )

| A. |
23米 |
B. |
24米 |
C. |
24.5米 |
D. |
25米 |
如图所示,某办公大楼正前方有一根高度是15米的旗杆 ,从办公楼顶端 测得旗杆顶端 的俯角 是 ,旗杆底端 到大楼前梯坎底边的距离 是20米,梯坎坡长 是12米,梯坎坡度 ,则大楼 的高度约为 (精确到0.1米,参考数据: , ,

| A. |
30.6 |
B. |
32.1 |
C. |
37.9 |
D. |
39.4 |
如图,坡面CD的坡比为 ,坡顶的平地BC上有一棵小树AB,当 太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC="3" 米,斜坡上的树影CD=
,坡顶的平地BC上有一棵小树AB,当 太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC="3" 米,斜坡上的树影CD= 米,则小树AB的高是 .
米,则小树AB的高是 .

如图,雨后初晴,李老师在公园散步,看见积水水面上出现梯步上方树的倒影,于是想利用倒影与物体的对称性测量这颗树的高度,他的方法是:测得树顶的仰角 、测量点 到水面平台的垂直高度 、看到倒影顶端的视线与水面交点 到 的水半距离 .再测得梯步斜坡的坡角 和长度 ,根据以下数据进行计算,
如图, 米, 米, 米, , .已知线段 和线段 关于直线 对称.(以下结果保留根号)
(1)求梯步的高度 ;
(2)求树高 .

如图, 是路边坡角为 ,长为10米的一道斜坡,在坡顶灯杆 的顶端 处有一探射灯,射出的边缘光线 和 与水平路面 所成的夹角 和 分别是 和 (图中的点 、 、 、 、 、 均在同一平面内, .
(1)求灯杆 的高度;
(2)求 的长度(结果精确到0.1米).(参考数据: . , ,

资阳市为实现 网络全覆盖, 年拟建设 基站七千个.如图,在坡度为 的斜坡 上有一建成的基站塔 ,小芮在坡脚 测得塔顶 的仰角为 ,然后她沿坡面 行走13米到达 处,在 处测得塔顶 的仰角为 .(点 、 、 、 均在同一平面内)(参考数据: , ,
(1)求 处的竖直高度;
(2)求基站塔 的高.
如图,某校教学楼后面紧邻着一个山坡,坡上面是一块平地. , ,斜坡 长 ,斜坡 的坡比为 .为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造.经地质人员勘测,当坡角不超过 时,可确保山体不滑坡.如果改造时保持坡脚 不动,则坡顶 沿 至少向右移 时,才能确保山体不滑坡.(取

如图,某商店营业大厅自动扶梯 的倾斜角为 , 的长为12米,则大厅两层之间的高度为 米.(结果保留两个有效数字)【参考数据; sin 31 ° = 0 . 515 , cos 31 ° = 0 . 857 , tan 31 ° = 0 . 601 】

如图,小刚从山脚 出发,沿坡角为 的山坡向上走了300米到达 点,则小刚上升了
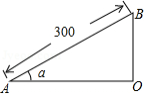
A. 米B. 米C. 米D. 米