如图,在平行四边形ABCD中,AB=5,BC=12,对角线交于点O,∠BAD的平分线交BC于E、交BD于F,分别过顶点B、D作AE的垂线,垂足为G、H,连接OG、OH.
(1)补全图形;
(2)求证:OG=OH;
(3)若OG⊥OH,直接写出∠OAF的正切值.
如图, 的半径为 ,其内接锐角三角形 中, 、 、 所对的边分别是 、 、 .
(1)求证: ;
(2)若 , , ,利用(1)的结论求 的长和 的值.

如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;
(3)如果BE=10,sinA= ,求⊙O的半径.
,求⊙O的半径.
已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为18,cosB= ,求DE的长.
,求DE的长.
如图,射线 和射线 相交于点 , ,且 .点 是射线 上的动点(点 不与点 和点 重合),作射线 ,并在射线 上取一点 ,使 ,连接 , .
(1)如图①,当点 在线段 上, 时,请直接写出 的度数;
(2)如图②,当点 在线段 上, 时,请写出线段 , , 之间的数量关系,并说明理由;
(3)当 , 时,请直接写出 的值.

如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管与支架CD所在直线相交于水箱横断面⊙O的圆心O,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=76厘米,∠CED=60°.
(1)求垂直支架CD的长度;(结果保留根号)
(2)求水箱半径OD的长度.(结果保留三个有效数字,参考数据: ≈1.414,
≈1.414, ≈1.73)
≈1.73)
如图,△ABC是直角三角形,∠ACB=90°.
(1)动手操作:利用尺规作∠ABC的平分线,交AC于点O,再以O为圆心,OC的长为半径作⊙O(保留作图痕迹,不写作法);
(2)综合运用:在你所作的图中,
①判断AB与⊙O的位置关系,并证明你的结论;
②若AC=12,tanOBC= ,求⊙O的半径.
,求⊙O的半径.
四边形 内接于 , 是 的直径, .
(1)如图1,求证 ;
(2)过点 作 的切线,交 延长线于点 (如图 .若 , ,求 的长.

如图,AB是高为60米的铁路,分别在河边D处测得塔顶A的仰角为60°,在与BD同一直线上的河对岸C处测得塔顶A的仰角为40°.
(1)求D点到铁塔距离DB的长;(结果保留根号)
(2)求河岸间CD的宽度.(结果取整数)
为测山高,在点A处测得山顶D的仰角为31°,从点A向山方向前进140米到达点B,在B处测得山顶D的仰角为62°(如图).
(1)在所给的图②中尺规作图:过点D作DC⊥AB,交AB的延长线于点C;
(2)山高DC是多少(结果取整数)?
如图,以 为直径的 经过 的顶点 ,过点 作 交 于点 ,交 于点 ,连接 交 于点 ,连接 ,在 的延长线上取一点 ,连接 ,使 .
(1)求证: 是 的切线;
(2)若 的半径是3, ,求 的长.

如图,厂房屋顶人字架的跨度BC=10m.D为BC的中点,上弦AB=AC,∠B=36°,求中柱AD和上弦AB的长(结果保留小数点后一位).
参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73.
如图,大楼AN上悬挂一条幅AB,小颖在坡面D处测得条幅顶部A的仰角为30°,沿坡面向下走到坡脚E处,然后向大楼方向继续行走10米来到C处,测得条幅的底部B的仰角为45°,此时小颖距大楼底端N处20米.已知坡面DE=20米,山坡的坡度i=1: (即tan∠DEM=1:
(即tan∠DEM=1: ),且D、M、E、C、N、B、A在同一平面内,E、C、N在同一条直线上,求条幅的长度(结果精确到1米)(参考数据:
),且D、M、E、C、N、B、A在同一平面内,E、C、N在同一条直线上,求条幅的长度(结果精确到1米)(参考数据: ≈1.73,
≈1.73,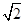 ≈1.41)
≈1.41)