广东省广州市越秀区初中毕业班综合测试数学试卷
地球绕太阳公转的速度约是110000千米/时,将110000用科学记数法表示为( )
| A.11×104 | B.1.1×104 | C.1.1×105 | D.0.11×106 |
若∠α与∠β互为补角,则下列式子成立的是( )
| A.α-β="90°" | B.α+β="90°" | C.α-β="180°" | D.α+β=180° |
下列运算正确的是( )
| A.x8÷x2=x6 | B.(x3y)2=x5y2 | C.-2(a-1)=-2a+1 | D.(x+3)2=x2+9 |
若代数式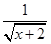 有意义,则实数x的取值范围是( )
有意义,则实数x的取值范围是( )
| A.x≥-2 | B.x>-2 | C.x≤-2 | D.x<-2 |
Rt△ABC中,∠C=90°,AC=3,BC=4,把它沿AC所在直线旋转一周,则所得几何体的侧面积是( )
| A.12π | B.15π | C.20π | D.36π |
如图,AB=AC,∠A=40°,AB的垂直平分线DE交AC于点E,垂足为D,则∠EBC的度数是( )
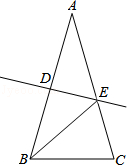
| A.30° | B.40° | C.70° | D.80° |
若关于x的一元二次方程x2+2x+k=0没有实数根,则一次函数y=(k-1)x+3的图象经过( )
| A.第二、三、四象限 | B.第一、二、三象限 |
| C.第一、三、四象限 | D.第一、二、四象限 |
如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AE•AD=AH•AF;其中结论正确的个数是( )
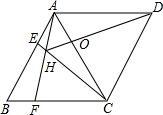
A.1个 B.2个 C.3个 D.4个
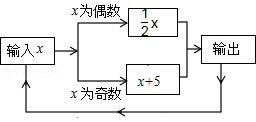
有一数值转换器,原理如图所示,若开始输入x的值是14,可发现第1次输出的结果是7,第2次输出的结果是12,依次继续下去,则第2015次输出的结果是 .
今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某数学兴趣小组在本校学生中做了一次抽样调查,调查结果共分为四个等级:A 非常了解;B 比较了解;C 基本了解;D 不了解.根据调查结果,绘制了如图的统计图,结合统计图,回答下列问题.
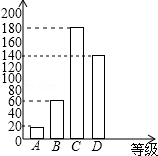
(1)本次抽样调查的样本容量是 ;
(2)若该校有学生1500人,请根据调查结果估计这些学生中“比较了解”雾霾天气知识的人数约为多少?
(3)根据调查结果,学校准备开展关于雾霾天气知识竞赛,某班要从“非常了解”的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:在一个不透明的袋中装有2个红球和2个白球,它们除了颜色外无其它差别,从中随机摸出两个球,若摸出的两个球颜色相同,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.
中国移动公司现推出两种移动电话计费方式:方式一:免月租费,本地通话费每分钟0.39元;方式二:月租费18元,本地通话费每分钟0.15元.
(1)若某用户选择方式一,本地通话时间为120分钟,则他应支付话费多少元?
(2)本地通话时间在什么范围时,选择方式二更合算?
如图,A(4,0),B(1,3),以OA、OB为边作平行四边形OACB,反比例函数y= 的图象经过点C.
的图象经过点C.
(1)求k的值;
(2)根据图象,直接写出y<3时自变量x的取值范围;
(3)将平行四边形OACB向上平移几个单位长度,使点B落在反比例函数的图象上.
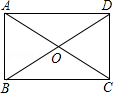
如图,△ABC是直角三角形,∠ACB=90°.
(1)动手操作:利用尺规作∠ABC的平分线,交AC于点O,再以O为圆心,OC的长为半径作⊙O(保留作图痕迹,不写作法);
(2)综合运用:在你所作的图中,
①判断AB与⊙O的位置关系,并证明你的结论;
②若AC=12,tanOBC= ,求⊙O的半径.
,求⊙O的半径.
如图,抛物线y=-x2-x+6与x轴交于A、B两点,与y轴交于点C.
(1)求点A、B的坐标;
(2)设点P是线段AC上一点,且S△ABP:S△BCP=1:3,求点P的坐标;
(3)若直线y= x+a与抛物线交于M、N两点,当∠MON为锐角时,求a的取值范围.
x+a与抛物线交于M、N两点,当∠MON为锐角时,求a的取值范围.

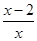 =3的解是 .
=3的解是 .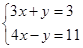 .
.
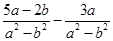 ,其中a=
,其中a=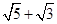 ,b=
,b=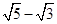 .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号